1. In a recent note I showed that Langmuir's adsorption isotherm

where θ is the fraction of the surface covered by adsorbed gas, p the gas pressure in equilibrium with it, and A (T) a specified function of the temperature, can be derived as a theorem in statistical mechanics without any appeal to the mechanism of deposition and re-evaporation. Necessary and sufficient assumptions for the truth of (1) are that the atoms (or molecules) of the gas are adsorbed as wholes on to definite points of attachment on the surface of the adsorber, that each point of attachment can accommodate one and only one adsorbed atom, and that the energies of the states of any adsorbed atom are independent of the presence or absence of other adsorbed atoms on neighbouring points of attachment. Under these assumptions the explicit form of (1) is

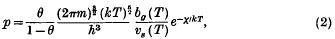
where m is the mass of the adsorbed atom or molecule, bg(T) the partition function for its internal states in the gas phase, and vs(T) the partition function for its set of adsorbed states. These sets of states are to be so specified that the energy zero is assigned tot the lowest state of each set in constructing bg(T) and vs(T), and then X is the energy required to transfer a molecule from the lowest adsorbed state tot the lowest gas state. Quite another adsorption isotherm was shown to hold when adsorption of a molecule takes place as atoms and requires two or more points of attachment.