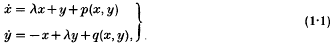Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Devlin, J.
1991.
Word problems related to derivatives of the displacement map.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 110,
Issue. 3,
p.
569.
Devlin, J.
1993.
Periodic solutions of polynomial non-autonomous differential equations.
Proceedings of the Royal Society of Edinburgh: Section A Mathematics,
Vol. 123,
Issue. 5,
p.
783.
Gaines, J. G.
1994.
The algebra of iterated stochastic integrals.
Stochastics and Stochastic Reports,
Vol. 49,
Issue. 3-4,
p.
169.
Christopher, C. J.
and
Devlin, J.
1997.
Isochronous Centers in Planar Polynomial Systems.
SIAM Journal on Mathematical Analysis,
Vol. 28,
Issue. 1,
p.
162.
Devlin, J.
Lloyd, N.G.
and
Pearson, J.M.
1998.
Cubic Systems and Abel Equations.
Journal of Differential Equations,
Vol. 147,
Issue. 2,
p.
435.
Briskin, M.
Francoise, J. -P.
and
Yomdin, Y.
2000.
Center conditions II: Parametric and model center problems.
Israel Journal of Mathematics,
Vol. 118,
Issue. 1,
p.
61.
Briskin, M.
Francoise, J. -P.
and
Yomdin, Y.
2000.
Center conditions III: Parametric and model center problems.
Israel Journal of Mathematics,
Vol. 118,
Issue. 1,
p.
83.
Devlin, James
2001.
Cyclicity of a critical point and the inverse Poincaré map.
Nonlinear Analysis: Theory, Methods & Applications,
Vol. 43,
Issue. 1,
p.
33.
Briskin, M.
Francoise, J.-P.
and
Yomdin, Y.
2001.
Operator Theory, System Theory and Related Topics.
p.
161.
Lijun, Yang
and
Yun, Tang
2001.
Some New Results on Abel Equations.
Journal of Mathematical Analysis and Applications,
Vol. 261,
Issue. 1,
p.
100.
Álvarez, M.J.
Bravo, J.L.
and
Fernández, M.
2009.
Uniqueness of limit cycles for polynomial first-order differential equations.
Journal of Mathematical Analysis and Applications,
Vol. 360,
Issue. 1,
p.
168.
Briskin, Miriam
Roytvarf, Nina
and
Yomdin, Yosef
2010.
Center conditions at infinity for Abel differential equations.
Annals of Mathematics,
Vol. 172,
Issue. 1,
p.
437.
Maite Grau
and
Xavier Santallusia
2013.
COMPOSITION CONDITIONS IN THE TRIGONOMETRIC ABEL EQUATION.
Journal of Applied Analysis & Computation,
Vol. 3,
Issue. 2,
p.
133.
Brudnyi, Alexander
2016.
Shuffle and Faà di Bruno Hopf algebras in the center problem for ordinary differential equations.
Bulletin des Sciences Mathématiques,
Vol. 140,
Issue. 7,
p.
830.
Ebrahimi-Fard, Kurusch
and
Gray, W. Steven
2016.
Center Problem, Abel Equation and the Faà di Bruno Hopf Algebra for Output Feedback.
International Mathematics Research Notices,
p.
rnw167.
Duffaut Espinosa, Luis A.
Ebrahimi-Fard, Kurusch
and
Gray, W. Steven
2018.
Discrete Mechanics, Geometric Integration and Lie–Butcher Series.
Vol. 267,
Issue. ,
p.
139.
Ebrahimi-Fard, Kurusch
and
Steven Gray, W.
2018.
Computation and Combinatorics in Dynamics, Stochastics and Control.
Vol. 13,
Issue. ,
p.
265.