Published online by Cambridge University Press: 24 October 2008
The function
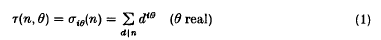
has had several applications in the analytic theory of numbers. It was used by Ingham [10] to give a new proof that ζ(1 + iθ) ≠ 0. In [1] we introduced the modern notation on the left above and used τ(n, θ) to show that for almost all n the numbers log d are asymptotically uniformly distributed (mod 1). If we define
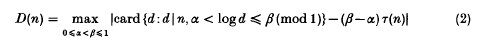
then it is known (Hall [2], Kátai[10]) that
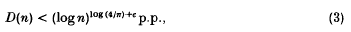
(where p.p. means ‘on a sequence of asymptotic density 1’). It is still an open problem whether or not we may strike out the term (log 4/π) = 0.24156 & from the exponent in (3).