Hostname: page-component-6dbcb7884d-vqfl6 Total loading time: 0 Render date: 2025-02-14T08:24:35.615Z Has data issue: false hasContentIssue false
  • English
  • Français

A table of n-component handlebody links of genus n+1 up to six crossings

Part of: Graph theory Low-dimensional topology

Published online by Cambridge University Press:  17 June 2022

GIOVANNI BELLETTINI ,
GIOVANNI PAOLINI ,
MAURIZIO PAOLINI  and
YI-SHENG WANG
GIOVANNI BELLETTINI
Affiliation:
Dipartimento di Ingegneria dell’Informazione e Scienze Matematiche, Università di Siena, 53100 Siena, Italy and International Centre for Theoretical Physics ICTP, Mathematics Section, 34151 Trieste, Italy. e-mail: [email protected]
GIOVANNI PAOLINI
Affiliation:
California Institute of Technology, Pasadena CA, U.S.A. (work done while at University of Fribourg, Department of Mathematics, 1700 Fribourg, Switzerland). e-mail: [email protected]
MAURIZIO PAOLINI
Affiliation:
Dipartimento di Matematica e Fisica, Università Cattolica del Sacro Cuore, 25121 Brescia, Italy. e-mail: [email protected]
YI-SHENG WANG
Affiliation:
Institute of Mathematics, Academia Sinica, Taipei 106, Taiwan. e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

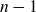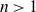A handlebody link is a union of handlebodies of positive genus embedded in 3-space, which generalises the notion of links in classical knot theory. In this paper, we consider handlebody links with a genus two handlebody and $n-1$ solid tori, $n>1$ . Our main result is the classification of such handlebody links with six crossings or less, up to ambient isotopy.

MSC classification

Primary: 57M15: Relations with graph theory
Secondary: 57M05: Fundamental group, presentations, free differential calculus 05C10: Planar graphs; geometric and topological aspects of graph theory
Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 174 , Issue 1 , January 2023 , pp. 199 - 223
Copyright
© The Author(s), 2022. Published by Cambridge University Press on behalf of Cambridge Philosophical Society

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bertuccioni, I.. A topological puzzle. Amer. Math. Monthly. 110 (2003), 937–939.Google Scholar
Bellettini, G., Paolini, M. and Wang, Y.-S.. Numerical irreducibility criteria for handlebody links. Topology Appl. 284 (2020), 107361, 14 pp.CrossRefGoogle Scholar
Botermans, J. and Van Delft, P.. Creative Puzzles of the World (Abrams, New York, 1975).Google Scholar
Brown, M.. Locally flat imbeddings of topological manifolds. Ann. Math., Second Series. 75, (1962), 331–341.CrossRefGoogle Scholar
Conway, J. H.. An enumeration of knots and links, and some of their algebraic properties, In Computational Problem in Abstract Algebra. Proc. Conf. Oxford. (1970), 329–358.CrossRefGoogle Scholar
Chongchitmate, W. and Ng, L.. An atlas of Legendrian knots. Exp. Math. 22 (2013), no. 1, 26–37.Google Scholar
Grushko, I. A.. On the bases of a free product of groups. Matematicheskii Sbornik. 8 (1940), 169–182.Google Scholar
Hirsch, M. W. and Mazur, B.. Smoothings of Piecewise Linear Manifolds , (AM-80) (Princeton University Press, Princeton, NJ, 1974).Google Scholar
Hoste, J., Thistlethwaite, M. and Weeks, J.. The first 1,701,936 knots. Math. Intelligencer 20 (1998), 33–48.CrossRefGoogle Scholar
Ishii, A.. Moves and invariants for knotted handlebodies. Algebr. Geom Topol. 8 (2008), 1403–1418.CrossRefGoogle Scholar
Ishii, A. and Iwakiri, M.. Quandle cocycle invariants for spatial graphs and knotted handlebodies. Canad. J. Math. 64 (2012), 102–122.Google Scholar
Ishii, A., Iwakiri, M., Jang, Y. and Oshiro, K.. A G-family of quandles and handlebody-knots. Illinois J. Math. 57 (2013), 817–838.Google Scholar
Ishii, A., Kishimoto, K., Moriuchi, H. and Suzuki, M.. A table of genus two handlebody-knots up to six crossings. J. Knot Theory Ramifications 21 (2012), no. 4, 1250035, 9 pp.CrossRefGoogle Scholar
Ishii, A., Kishimoto, K. and Ozawa, M.. Knotted handle decomposing spheres for handlebody-knots. J. Math. Soc. Japan 67 (2015), 407–417.Google Scholar
Kauffman, L. H.. Invariants of graphs in three-space. Trans. Amer. Math. Soc. 311 (1989), no. 2, 679–710.Google Scholar
Kitano, T. and Suzuki, M.. On the number of $SL(2,\mathbb{Z}/p\mathbb{Z})$ -representations of knot groups. J. Knot Theory Ramifications. 21 (2012), no. 1, 1250003, 18 pp.CrossRefGoogle Scholar
Koda, Y. and Ozawa, M., with an appendix by C. Gordon. Essential surfaces of non-negative Euler characteristic in genus two handlebody exteriors. Trans. Amer. Math. Soc. 367 (2015), no. 4, 2875–2904.CrossRefGoogle Scholar
Lackenby, M.. The crossing number of composite knots. J. Topol. 2 (4) (2009), 747–768.CrossRefGoogle Scholar
Lee, J. H. and Lee, S.. Inequivalent handlebody-knots with homeomorphic complements. Algebr. Geom. Topol. 12 (2012), 1059–1079.CrossRefGoogle Scholar
Malyutin, A. V.. On the question of genericity of hyperbolic knots. Int. Math. Res. Notices. (2018), 1073–7928.Google Scholar
Melvin, P.. A topological menagerie. Amer. Math. Monthly. 113 (2006), 348–351.Google Scholar
Mizusawa, A.. Linking numbers for handlebody-links. Proc. Japan Acad. 89, Ser. A (2013), 60–62.CrossRefGoogle Scholar
Moriuchi, H.. An enumeration of theta-curves with up to seven crossings. J. Knot Theory Ramifications. 18 (2009), 67–197.Google Scholar
Moriuchi, H.. A table of handcuff graphs with up to seven crossings. OCAMI Studies Vol 1. Knot Theory for Scientific objects (2007), 179–300.Google Scholar
Moriuchi, H.. A table of $\theta$ -curves and handcuff graphs with up to seven crossings. Adv. Stud. Pure Math. Noncommutativity and Singularities: Proceedings of French–Japanese symposia held at IHES in 2006, J.-P. Bourguignon, M. Kotani, Y. Maeda and N. Tose, eds. (Tokyo: Mathematical Society of Japan, 2009), 281–290.Google Scholar
Motto, M.. Inequivalent genus two handlebodies in $S^{3}$ with homeomorphic complements. Topology Appl. 36(3) (1990), 283–290.CrossRefGoogle Scholar
Munkres, J.. Elementary Differential Topology , (AM-54). (Princeton University Press, Princeton, NJ, 1966).Google Scholar
Paolini, M.. Appcontour. Computer software. Vers. 2.5.3. Apparent contour, (2018) $<$ http://appcontour.sourceforge.net/ $>$ .$+.>Google Scholar
Rolfsen, D.. Knots and Links . (AMS Chelsea Publishing, vol. 364, 2003).Google Scholar
Rourke, C. P. and Sanderson, B. J.. Introduction to Piecewise-Linear Topology. (Springer-Verlag, Berlin-New York, 1982).Google Scholar
Suzuki, S., On surfaces in 3-sphere: prime decompositions. Hokkaido Math. J. 4 (1975), 179–195.CrossRefGoogle Scholar
Tsukui, Y., On surfaces in 3-space. Yokohama Math. J. 18 (1970), 93–104.Google Scholar
Tsukui, Y., On a prime surface of genus 2 and homeomorphic splitting of 3-sphere. Yokohama Math. J. 23 (1975), 63–75.Google Scholar
Whitney, H., Congruent graphs and the connectivity of graphs. Amer. J. Math. 54 (1932), 150–168.CrossRefGoogle Scholar
Yetter, D. N., Category theoretic representations of knotted graphs in $S^3$ . Adv. Math. 77 (1989), 137–155.CrossRefGoogle Scholar