Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
JEONG, MYEONG-JU
KIM, EUN-JIN
and
PARK, CHAN-YOUNG
2004.
TWIST MOVES AND VASSILIEV INVARIANTS.
Journal of Knot Theory and Its Ramifications,
Vol. 13,
Issue. 06,
p.
719.
STOIMENOW, Alexander
2007.
5-moves and Montesinos links.
Journal of the Mathematical Society of Japan,
Vol. 59,
Issue. 3,
Duzhin, S. V.
2011.
Proof of Przytycki’s conjecture on matched diagrams.
Doklady Mathematics,
Vol. 84,
Issue. 3,
p.
787.
Nakanishi, Yasutaka
Sakamoto, Yoko
and
Satoh, Shin
2015.
Delta-crossing number for knots.
Topology and its Applications,
Vol. 196,
Issue. ,
p.
771.
Jeong, Myeong-Ju
Choi, Younhee
and
Kim, Dojin
2022.
Twist moves and the affine index polynomials of virtual knots.
Journal of Knot Theory and Its Ramifications,
Vol. 31,
Issue. 07,


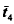 moves conjecture for oriented links with matched diagrams
moves conjecture for oriented links with matched diagrams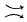 by
by 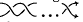 is called a
is called a 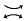 by
by 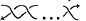 is called a
is called a 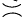 by
by 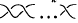 for any
for any 