Published online by Cambridge University Press: 24 October 2008
Nous ne considérerons, en général, que les sous-ensembles de l'intervalle [0, 1] et nous désignerons par 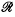 et
et 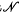 respectivement l'ensemble des nombres rationnels et l'ensemble des nombres irrationnels de cet intervalle.
respectivement l'ensemble des nombres rationnels et l'ensemble des nombres irrationnels de cet intervalle.
Nous allons employer pour les fractions continues la notation
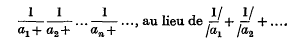
Étant donnée une suite de nombres naturels {zn}, nous dirons que le nombre 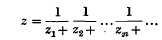 correspond à la suite {zn} et vice versa, et nous écrironns z = v({zn}). Pareillement, nous dirons qu'un ensemble
correspond à la suite {zn} et vice versa, et nous écrironns z = v({zn}). Pareillement, nous dirons qu'un ensemble 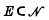 correspond à une famille Φ de suites de nombres naturels si l'on a E = v(Φ).
correspond à une famille Φ de suites de nombres naturels si l'on a E = v(Φ).
† Fund. Math. 32 (1939), 294–300.Google Scholar Cette note sera désignée dans ce qui suit par “F.M. 32” (p. ex. “lemme 3, F.M. 32”). Nous en empruntons ici les lemmes 1 et 3 et le théorème 1. Pour renseignements générals, voir Sierpiński, W., Hypothèse du continu, Monografie matematyczne 4 (Warszawa-Lwów, 1934).Google Scholar
† Besicovitch, A. S., Acta Math. 62 (1934), 289.CrossRefGoogle Scholar Voir aussi Sierpiński, W., Fund. Math. 32 (1939), 301CrossRefGoogle Scholar et Szpilrajn, E., Fund. Math. 31 (1938), 219.CrossRefGoogle Scholar
‡ Hausdorff, F., “Summen von ℵ Mengen”, Fund. Math. 26 (1936), 247.CrossRefGoogle Scholar
§ Puisque, en vertu d'un théorème de M. Besicovitch, tout ensemble concentré jouit de la propriété C.
∥ Rothberger, F., Fund. Math. 30 (1938), 50,CrossRefGoogle ScholarSierpiński, W., Fund. Math. 30 (1938), 56.CrossRefGoogle Scholar Pour les définitions voir, plus loin, § 2, p. 113.
¶ Fund. Math. 30 (1938), 58.Google Scholar Pour la définition de la propriété λ voir § 1, p. iii.
†† Fund. Math. 25 (1935), 579.Google Scholar
‡‡ Sierpiński, W., Fund. Math. 30 (1938), 58.Google Scholar §§ Loc. cit.
† Sierpiński, W., Hypothèse du continu, Monografie Matematyczne 4 (Warszawa-Lwów, 1934), 53.Google Scholar
‡ Voici l'énoncé du lemme 3 de F.M. 32: E étant un sous-ensemble quelconque de N, la famille des suites correspondant à E est bornée ou non, suivant que ![]() est ou n'est pas un G srelativement à E +
est ou n'est pas un G srelativement à E + ![]() .
.
§ Sierpiński, W., Fund. Math. 32 (1939), 301.CrossRefGoogle Scholar
† En vertu d'un théorème de M. Mazurkiewicz (voir Kuratowski, C., Topologie, 1, Monografie Matematyczne 3 (Warszawa-Lwów 1933, 255,Google Scholar th. 3) tout G δ linéaire qui est dense et frontière est homéomorphe à N.
† Lemme 1, F.M. 32.
‡ Voir Kuratowski, C., Topologie, 1, 270Google Scholar (ou bien notre lemma 4, F.M. 32).
§ Cf. Sierpiński, W., Fund. Math. 29 (1937), 91,Google Scholar où l'on trouvera une liste de travaux antérieurs concernant la propriété C.
† Rothberger, F., Fund. Math. 30 (1938), 50.CrossRefGoogle Scholar
‡ La démonstration de ce lemme est la même que celle du “Satz 3”, loc. cit. p. 52.
Nous y avons, en effet, montré que, si un ensemble X est dépourvu de la propriété C′, il existe une fonction f(x) continue dans X telle que f(X) soit dépourvu de la propriété C. D'autre part, toute image continue d'un ensemble à propriété C′ jouit de la propriété C (Satz 1, Satz 2, loc. cit.).
§ Rothberger, F., Fund. Math. 30 (1938), 54.Google Scholar
∥ A. S. Besicovitch, loc. cit., Sierpinski, W., Fund. Math. 30 (1938), 58.Google Scholar
† Sierpiński, W., C.R. Soc. Sci. Varsovie, 30 (1937), 10.Google Scholar
‡ Fund. Math. 25 (1935), 579.Google Scholar
§ Sierpiński, W., Fund. Math. 30 (1938), 56.CrossRefGoogle Scholar
∥ Sierpiński, W. et Szpilrajn, E., Fund. Math. 26 (1936), 257.Google Scholar
† Voir, à ce sujet, W. Sierpiński, Hypothèse du continu, chapitre 2: “Ensemble de M. Lusin.”
‡ Dans cet ordre d'idées, on a encore quelques autres équivalences: on peut remplacer la proposition 2°, ou bien par la proposition (K):
Tout ensemble de puissance inférieure à cells du continu est de première catégorie (Sierpiński, W., Hypothèse du continu, p. 29,Google Scholar proposition P9), ou bien par la proposition suivante:
Il existe un ensemble indénombrable jouissant de la propriété S,c. à d. presqu'héréditairement non-mesurable (Rothberger, F., Fund. Math. 30 (1938), 215CrossRefGoogle Scholar), ou encore par celle-ci (proposition (T*)):
Il existe une fonction qui transforms d'une façon biunivoque la droite en elle-même en transformant tout ensemble de mesure nulle en un ensemble de première catégorie (Sierpiński, W., Fund. Math. 32 (1939), 257)Google Scholar.
Le problème, si la proposition L, seule, équivaut à l'hypothèse du continu, reste ouvert.
† Hausdorff, F., Fund. Math. 26 (1936), 243–4.CrossRefGoogle Scholar
† Cf. p. 121.