Hostname: page-component-586b7cd67f-rdxmf Total loading time: 0 Render date: 2024-11-26T07:45:32.588Z Has data issue: false hasContentIssue false
  • English
  • Français

The support of tempered distributions

Published online by Cambridge University Press:  01 March 2008

Colin C. Graham
Colin C. Graham*
Affiliation:
Department of Mathematics, University of British ColumbiaMailing address: RR#1–D156, Bowen Island, BC, V0N 1G0Canada. e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We identify the support of a tempered distribution by evaluation of a sequence of test functions against the Fourier transform of the distribution. This improves previous results by removing the restriction that the distribution's Fourier transform be in 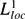and be of polynomial growth. We use an apparently new technical lemma that implies that certain bounded approximate identities for 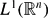are also topological approximate identities for elements of the space 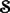of Schwartz functions.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 144 , Issue 2 , March 2008 , pp. 495 - 498
Copyright
Copyright © Cambridge Philosophical Society 2008

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]González Vieli, F. J.Intégrales trigonométriques et pseudofonctions. Ann. Inst. Fourier 44 (1994), 197–211.Google Scholar
[2]González Vieli, F. J.Inversion de Fourier ponctuelle des distributions à support compact. Arch. Math. (Basel) 75 (2000), 290–298.CrossRefGoogle Scholar
[3]Vieli, F. J. González. Characterization of the support of pseudomeasures on ℝ. Math. Proc. Camb. Phil. Soc. 135 (2003), 431–442.Google Scholar
[4]González Vieli, F. J. and Graham, C. C.. On the support of tempered distributions. Arch. Math. (Basel) 88 (2007), No. 2, 133–142.CrossRefGoogle Scholar
[5]Graham, C. C.. The support of pseudomeasures on ℝ. Math. Proc. Camb. Phil. Soc. 142 (2007), No. 1, 149–152.CrossRefGoogle Scholar
[6]Kahane, J.-P. and Salem, R.Ensembles Parfaits et Séries Trigonométriques (Hermann, 1963) (Nouvelle Édition 1994).Google Scholar
[7]Schwartz, L.Théorie des Distributions, II (Hermann, 1951).Google Scholar
[8]Stein, E. M. and Weiss, G.Introduction to Fourier Analysis on Euclidean Spaces (Princeton University Press, 1971).Google Scholar
[9]Walter, G.Pointwise convergence of distribution expansions. Studia Math. 26 (1966), 143–154.Google Scholar