Hostname: page-component-78c5997874-j824f Total loading time: 0 Render date: 2024-11-07T02:14:32.079Z Has data issue: false hasContentIssue false
  • English
  • Français

Subsequence principles for vector-valued random variables

Published online by Cambridge University Press:  24 October 2008

D. J. H. Garling
D. J. H. Garling
Affiliation:
St John's College, Cambridge
Get access Rights & Permissions [Opens in a new window]

Extract

1. Introduction. Révész(8) has shown that if (fn) is a sequence of random variables, bounded in L2, there exists a subsequence (fnk) and a random variable f in L2 such that 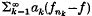converges almost surely whenever 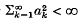. Komlós(5) has shown that if (fn) is a sequence of random variables, bounded in L1, then there is a subsequence (A*) with the property that the Cesàro averages of any subsequence converge almost surely. Subsequently Chatterji(2) showed that if (fn) is bounded in LP (where 0 < p ≤ 2) then there is a subsequence (gk) = (fnk) and f in Lp such that

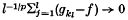
almost surely for every sub-subsequence. All of these results are examples of subsequence principles: a sequence of random variables, satisfying an appropriate moment condition, has a subsequence which satisfies some property enjoyed by sequences of independent identically distributed random variables. Recently Aldous(1), using tightness arguments, has shown that for a general class of properties such a subsequence principle holds: in particular, the results listed above are all special cases of Aldous' principal result.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 86 , Issue 2 , September 1979 , pp. 301 - 312
Copyright
Copyright © Cambridge Philosophical Society 1979

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

(1)Aldous, D. J.Limit theorems for subsequences of arbitrarily-dependent sequences of random variables. Z. Wahrscheinlichkeitstheorie und Verw. Gebiete 40 (1977), 59–82.CrossRefGoogle Scholar
(2)Chatterji, S. D.A general strong law. Invent. Math. 9 (1970), 235–245.CrossRefGoogle Scholar
(3)Diestel, J. Geometry of Banach spaces – selected topics. Lecture Notes in Mathematics, no. 485 (Springer-Verlag 1975).Google Scholar
(4)Figiei, T.On the moduli of convexity and smoothness. Studio Math. 56 (1976), 121–155.CrossRefGoogle Scholar
(5)KomlóS, J.A generalization of a problem of Steinhaus. Acta Math. Acad. Sci. Hungar. 18 (1967), 217–229.CrossRefGoogle Scholar
(6)Meyer, P. A. Martingales and stochastic integrals: I. Lecture Notes in Mathematics, no. 284 (Springer-Verlag, 1972).Google Scholar
(7)Pisier, G.Martingales with values in uniformly convex spaces. Israel J. Math. 20 (1975), 326–350.CrossRefGoogle Scholar
(8)Révész, P.On a problem of Steinhaus. Acta Math. Acad. Sci. Hungar. 16 (1965), 310–318.Google Scholar
(9)Suchanek, A. M. On almost sure convergence of averages of subsequences of vector-valued functions. (Preprint.)Google Scholar