Throughout this paper we deal only with complex and semi-simple algebras. Let B be such an algebra. We denote the socle of B as SB. B is a modular annihilator algebra if B/SB is a radical algebra, i.e. if every element of B is quasi-regular modulo the socle of B; see (1) or (12). Now assume that B is a modular annihilator algebra and a Banach algebra. Then any semi-simple closed subalgebra of B is a modular annihilator algebra by ((4), Cor. to Theorem 4·2,). It is not true, however, that any semi-simple subalgebra A of B is a modular annihilator algebra, even when A is a Banach algebra in some norm. We give a simple example to illustrate this. Let A be the algebra of all complex functions f, continuous on the closed unit disk D in the complex plane, analytic in the interior of D, and such that f(0) = 0. A is a Banach algebra in the usual sup norm over D. Now consider the norm on A defined by

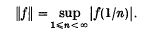
Let B be the completion of A in this norm. A has an involution * defined by 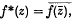and also ‖ff*‖ = ‖f‖2 for all f ∈ A. Therefore B is a B*-algebra. It is not difficult to verify that the only non-zero multiplicative linear functionals on A which are continuous with respect to the norm ‖·‖, are the point evaluations at 1/n, n = 1, 2 …. It follows that every non-zero multiplicative linear functional on B is an extension of one of these point evaluations to B. Thus B can be identified with the algebra of all complex sequences which converge to zero.