Hostname: page-component-586b7cd67f-g8jcs Total loading time: 0 Render date: 2024-11-26T08:38:13.506Z Has data issue: false hasContentIssue false
  • English
  • Français

Spherically symmetric differential equations, the rotation group, and tensor spherical functions

Published online by Cambridge University Press:  24 October 2008

R. Burridge
R. Burridge
Affiliation:
King's College, Cambridge
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper a scheme is developed for handling tensor partial differential equations having spherical symmetry. The basic technique is that of Gelfand and Shapiro ((2), §8) by which tensor fields defined on a sphere give rise to scalar fields defined on the rotation group 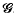. These fields may be expanded as series of functions 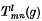, where 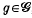, m is fixed and the matrices Tl(g) form a 21 + 1 dimensional irreducible representation of .

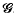Spherically symmetric operations, such as covariant differentiation of tensors and the contraction of tensors with other spherically symmetric tensor fields, are shown to act in a particularly simple way on the terms of the series mentioned above: terms with given l, n are transformed into others with the same values of l, n. That this must be so follows from Schur's Lemma and the fact that for each m and l the functions 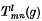form a basis for an invariant subspace of functions on 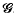of dimension 2l + 1 in which an irreducible representation of 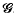acts. Explicit formulae for the results of such operations are presented.

The results are used to show the existence of scalar potentials for tensors of all ranks and the results for tensors of the second rank are shown to be closely related to those recently obtained by Backus(1).

This work is intended for application in geophysics and other fields where spherical symmetry plays an important role. Since workers in these fields may not be familiar with quantum theory, some matter in sections 2–5 has been included in spite of the fact that it is well known in the quantum theory of angular momentum.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 65 , Issue 1 , January 1969 , pp. 157 - 175
Copyright
Copyright © Cambridge Philosophical Society 1969

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Backus, G. E.Potentials for tangent tensor fields on spheroids. Arch. Rational Mech. Anal. 22 (1966), no. 3, 210–252.CrossRefGoogle Scholar
(2)Gelfand, I. M. and Shapiro, Z. Ya.Representations of the group of rotations in three-dimensional space and their applications. Amer. Math. Soc. Transl. 2 (1956), 207–316.Google Scholar
(3)Gelfand, I. M., Minlos, R. A. and Shapiro, Z. Ya.Representations of the rotation and Lorentz groups and their applications (Pergamon, London, 1963).Google Scholar
(4)Goldstein, H.Classical mechanics (Addison-Wesley, Reading, Mass., 1950).Google Scholar
(5)Morse, P. M. and Feshbach, H.Methods of theoretical physics. Part 2 (McGraw-Hill, New York, 1953).Google Scholar
(6)Rose, M. E.Elementary theory of angular momentum (John Wiley and Sons, New York, 1957).Google Scholar
(7)Synge, J. L.Classical dynamics, in Encyclopedia of Physics, Ed. Flugge, S., vol. III/1 (Springer, Berlin, 1960).Google Scholar