Hostname: page-component-78c5997874-fbnjt Total loading time: 0 Render date: 2024-11-16T18:03:34.467Z Has data issue: false hasContentIssue false
  • English
  • Français

Spectral manifolds for the perturbed Schrödinger operator in Lp (Rn)†

Published online by Cambridge University Press:  24 October 2008

M. Thompson
M. Thompson
Affiliation:
University of Sussex
Get access Rights & Permissions [Opens in a new window]

Extract

In a recent paper(14), Talenti gave a complete characterization of the spectrum of the maximal realization Hop of − Δ in Lp(Rn), for p in the range

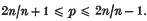
Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 77 , Issue 2 , March 1975 , pp. 369 - 383
Copyright
Copyright © Cambridge Philosophical Society 1975

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Alsholm, P. and Schmidt, G.Spectral and Scattering theory for Schrödinger operators. Various Publications Series, Mathematisk Institut, Aarhus Universitet, 7 (1969).Google Scholar
(2)Agmon, S.Lower bounds for solutions of Schrödinger equations. J. Analyse Math. 23 (1970) 1–25.CrossRefGoogle Scholar
(3)Agmon, S. Uniqueness results for solutions of differential equations in Hilbert space with applications to problems in partial differential equations. Lecture series in differential equations, vol. II, edited Aziz, A. K. (Van Nostrand, New York, 1969).Google Scholar
(4)Balslev, E.The singular spectrum of elliptic differential operators in Lp(Rn). Math. Scand. 19 (1966), 193–210.CrossRefGoogle Scholar
(5)Bartle, R. G.Spectral decomposition of operators in Banach spaces. Proc. London Math. Soc. 20 (1970), 438–450.Google Scholar
(6)Browder, F.On the spectral theory of elliptic differential operators, I. Math. Ann. 142 (1961), 22–130.Google Scholar
(7)Eidus, D. M.The principle of limit amplitude. Trans. Amer. Math. Soc. 47 (1965), 156–192.Google Scholar
(8)Faris, W. G.Time decay and the Born series. Rocky Mountain J. Math. 1 (1971), 637–648.CrossRefGoogle Scholar
(9)Kocan, D.Spectral manifolds for a class of operators. Illinois J. Math. 10 (1966), 605–622.Google Scholar
(10)Kato, T.Wave operators and similarity for some non-selfadjoint operators. Math. Ann. 162 (1966), 258–279.Google Scholar
(11)Murray, F. J.Quasi-complements and closed projections in reflexive Banach spaces. Trans. Amer. Math. Soc. 58 (1945), 77–95.Google Scholar
(12)Okikiolu, G. O.Aspects of the Theory of Bounded Integral Operators in Lp spaces (Academic Press, New York, 1971).Google Scholar
(13)Schechter, M.On the essential spectrum of an arbitrary operator, I. J. Math. Anal. Appl. 13 (1966), 205–215.CrossRefGoogle Scholar
(14)Talenti, G. Spectrum of the Laplace operator acting in Lp(Rn). Institute Nazionale di Alta Matematica, Symposia Mathernatica, vol. VII (Bologna, 1971).Google Scholar
(15)Thompson, M.Spectral manifolds for constant coefficient elliptic operators in Lp(Rn). To appear. Proc. Roy. Soc. Edinburgh.Google Scholar
(16)Yosida, K.Functional analysis, Band 123 (Springer-Verlag, Berlin, 1966).Google Scholar