Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Brown, Gavin
1978.
Integrability of Fourier transforms under an ergodic hypothesis.
Journal of the Australian Mathematical Society,
Vol. 26,
Issue. 2,
p.
129.
Berg, Christian
1979.
Probability Measures on Groups.
Vol. 706,
Issue. ,
p.
10.
Bott, R. T.
1983.
Singularity of generalised Riesz products.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 93,
Issue. 2,
p.
335.
Freedman, David
and
Pitman, Jim
1990.
A measure which is singular and uniformly locally uniform.
Proceedings of the American Mathematical Society,
Vol. 108,
Issue. 2,
p.
371.
Doubtsov, Evgueni
2000.
Little Bloch Functions, Symmetric Pluriharmonic Measures, and Zygmund's Dichotomy.
Journal of Functional Analysis,
Vol. 170,
Issue. 2,
p.
286.
Benedetto, John J.
Bernstein, Erica
and
Konstantinidis, Ioannis
2005.
Multiscale Riesz Products and their Support Properties.
Acta Applicandae Mathematicae,
Vol. 88,
Issue. 2,
p.
201.
EL ABDALAOUI, E. H.
and
NADKARNI, M. G.
2016.
A non-singular transformation whose spectrum has Lebesgue component of multiplicity one.
Ergodic Theory and Dynamical Systems,
Vol. 36,
Issue. 3,
p.
671.
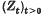 of symmetric random variables which satisfy inter alia the following properties:
of symmetric random variables which satisfy inter alia the following properties: