Hostname: page-component-586b7cd67f-t8hqh Total loading time: 0 Render date: 2024-11-26T08:41:36.108Z Has data issue: false hasContentIssue false
  • English
  • Français

Sets with large intersection and ubiquity

Published online by Cambridge University Press:  01 January 2008

ARNAUD DURAND
ARNAUD DURAND*
Affiliation:
Laboratoire d'Analyse et de Mathématiques Appliquées, Université Paris XII, 61 av. du Général de Gaulle, 94010 Créteil Cedex, France. e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

A central problem motivated by Diophantine approximation is to determine the size properties of subsets of 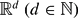of the form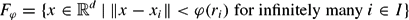where ‖⋅‖ denotes an arbitrary norm, I a denumerable set, (xi,ri)i∈ I a family of elements of 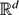× (0, ∞) and ϕ a nonnegative nondecreasing function defined on [0, ∞). We show that if FId, where Id denotes the identity function, has full Lebesgue measure in a given nonempty open subset V of 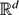, the set Fϕ belongs to a class Gh(V) of sets with large intersection in V with respect to a given gauge function h. We establish that this class is closed under countable intersections and that each of its members has infinite Hausdorff g-measure for every gauge function g which increases faster than h near zero. In particular, this yields a sufficient condition on a gauge function g such that a given countable intersection of sets of the form Fϕ has infinite Hausdorff g-measure. In addition, we supply several applications of our results to Diophantine approximation. For any nonincreasing sequence ψ of positive real numbers converging to zero, we investigate the size and large intersection properties of the sets of all points that are ψ-approximable by rationals, by rationals with restricted numerator and denominator and by real algebraic numbers. This enables us to refine the analogs of Jarník's theorem for these sets. We also study the approximation of zero by values of integer polynomials and deduce several new results concerning Mahler's and Koksma's classifications of real transcendental numbers.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 144 , Issue 1 , January 2008 , pp. 119 - 144
Copyright
Copyright © Cambridge Philosophical Society 2008

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Aubry, J.-M. and Jaffard, S.. Random wavelet series. Comm. Math. Phys 227 (2002), no. 3, 483–514.Google Scholar
[2]Baker, A. and Schmidt, W. M.. Diophantine approximation and Hausdorff dimension. Proc. London Math. Soc 21 (1970), no. 3, 1–11.Google Scholar
[3]Beresnevich, V. V.. On approximation of real numbers by real algebraic numbers. Acta Arith 90 (1999), no. 2, 97–112.CrossRefGoogle Scholar
[4]Beresnevich, V. V.. Application of the concept of regular systems of points in metric number theory. Vests = i Nats. Akad. Navuk Belarus = i Ser. F = i z.-Mat. Navu 1 (2000), 35–39.Google Scholar
[5]Beresnevich, V. V.. On a theorem of V. Bernik in the metric theory of Diophantine approximation. Acta Arith 117 (2005), no. 1, 71–80.CrossRefGoogle Scholar
[6]Beresnevich, V. V., Bernik, V. I. and Dodson, M. M.. Regular systems, ubiquity and Diophantine approximation. In A Panorama of Number Theory or The View From Baker's Garden (Cambridge University Press, 2002), pp. 260–279.CrossRefGoogle Scholar
[7]Beresnevich, V. V., Dickinson, D. and Velani, S. L.. Measure theoretic laws for limsup sets. Mem. Amer. Math. Soc 179 (2006), no. 846, 1–91.Google Scholar
[8]Beresnevich, V. V. and Velani, S. L.. A mass transference principle and the Duffin–Schaeffer conjecture for Hausdorff measures. Ann. Math. (2) 164 (2006), no. 3, 971–992.CrossRefGoogle Scholar
[9]Bernik, V. I.. The exact order of approximating zero by values of integral polynomials. Acta Arith 53 (1989), no. 1, 17–28.Google Scholar
[10]Besicovitch, A. S.. Sets of fractional dimensions (IV): on rational approximation to real numbers. J. London Math. Soc 9 (1934), 126–131.Google Scholar
[11]Bugeaud, Y.. Approximation by algebraic integers and Hausdorff dimension. J. London Math. Soc. (2) 65 (2002), no. 3, 547–559.CrossRefGoogle Scholar
[12]Bugeaud, Y.. Approximation par des nombres algébriques de degré borné et dimension de Hausdorff. J. Number Theor 96 (2002), no. 1, 174–200.CrossRefGoogle Scholar
[13]Bugeaud, Y.. Approximation by Algebraic Numbers. Cambridge Tracts in Mathematics. no. 160 (Cambridge University Press, 2004).Google Scholar
[14]Bugeaud, Y.. An inhomogeneous Jarník theorem. J. Anal. Math 92 (2004), 327–349.Google Scholar
[15]Bugeaud, Y.. Intersective sets and Diophantine approximation. Michigan Math. J 52 (2004), no. 3, 667–682.Google Scholar
[16]Dodson, M. M., Rynne, B. P. and Vickers, J. A. G.. Diophantine approximation and a lower bound for Hausdorff dimension. Mathematik 37 (1990), no. 1, 59–73.CrossRefGoogle Scholar
[17]Durand, A.. Singularity sets of Lévy processes. Preprint (2007).Google Scholar
[18]Hos, P. Erd. Representations of real numbers as sums and products of Liouville numbers. Michigan Math. J 9 (1962), 59–60.Google Scholar
[19]Falconer, K. J.. Classes of sets with large intersection. Mathematik 32 (1985), no. 2, 191–205.CrossRefGoogle Scholar
[20]Falconer, K. J.. Sets with large intersection properties. J. London Math. Soc. (2) 49 (1994), no. 2, 267–280.CrossRefGoogle Scholar
[21]Falconer, K. J.. Fractal Geometry: Mathematical Foundations and Applications. 2nd ed. (Wiley, 2003).Google Scholar
[22]Hardy, G. H. and Wright, E. M.. An Introduction to the Theory of Numbers. 5th ed. (Oxford University Press, 1979).Google Scholar
[23]Harman, G.. Metric number theory. LMS Monographs (N.S.). vol. 18 (Clarendon Press, 1998).CrossRefGoogle Scholar
[24]Jaffard, S.. On lacunary wavelet series. Ann. Appl. Probab 10 (2000), no. 1, 313–329.Google Scholar
[25]Jarník, V.. Diophantischen Approximationen und Hausdorffsches Mass. Mat. Sbor 36 (1929), 371–381.Google Scholar
[26]Jarník, V.. Über die simultanen Diophantischen Approximationen. Math. Z 33 (1931), 505–543.Google Scholar
[27]Khintchine, A. I.. Zur metrischen Theorie der diophantischen Approximationen. Math. Z 24 (1926), 706–714.Google Scholar
[28]Koksma, J. F.. Über die Mahlersche Klasseneinteilung der transzendenten Zahlen und die Approximation komplexer Zahlen durch algebraische Zahlen. Monatsh. Math. Phys 48 (1939), 176–189.Google Scholar
[29]Levesley, J.. A general inhomogeneous Jarník-Besicovitch theorem. J. Number Theor 71 (1998), no. 1, 65–80.CrossRefGoogle Scholar
[30]Mahler, K.. Zur Approximation der Exponentialfunktionen und des Logarithmus. J. Reine Angew. Math 166 (1932), 118–150.Google Scholar
[31]Olsen, L.. On the exact Hausdorff dimension of the set of Liouville numbers. Manuscripta Math 116 (2005), no. 2, 157–172.Google Scholar
[32]Olsen, L. and Renfro, D. L.. On the exact Hausdorff dimension of the set of Liouville numbers II. Manuscripta Math 119 (2006), no. 2, 217–224.Google Scholar
[33]Rogers, C. A.. Hausdorff Measures (Cambridge University Press, 1970).Google Scholar
[34]Schmidt, W. M.. Metrical theorems on fractional parts of sequences. Trans. Amer. Math. Soc 110 (1964), 493–518.Google Scholar
[35]Schneider, T.. Einführung in die Transzendenten Zahlen (Springer, 1957).CrossRefGoogle Scholar
[36]Sprindžuk, V. G.. Mahler's Problem in Metric Number Theory (Amer. Math. Soc., 1969).Google Scholar
[37]Wirsing, E.. Approximation mit algebraischen Zahlen beschränkten Grades. J. Reine Angew. Math 206 (1961), 67–77.Google Scholar