Hostname: page-component-669899f699-8p65j Total loading time: 0 Render date: 2025-04-25T20:41:39.643Z Has data issue: false hasContentIssue false
  • English
  • Français

Series in locally convex spaces and inclusions between FK spaces

Published online by Cambridge University Press:  24 October 2008

I. J. Maddox
I. J. Maddox
Affiliation:
The Queen's University of Belfast
Get access Rights & Permissions [Opens in a new window]

Extract

Singer [10] defined a series Σxk in a Banach space X to be weakly p-unconditionally Cauchy if and only if Σλkxk converges in X for all λ∊lp, where 1 < p < ∞. For Banach spaces containing no subspace isomorphic to c0 Singer characterized such series as those for which

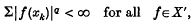
where 1/p + 1/q = 1 and X′ is the dual space of X.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 95 , Issue 3 , May 1984 , pp. 467 - 472
Copyright
Copyright © Cambridge Philosophical Society 1984

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

REFERENCES

[1]Bennett, G.. Some inclusion theorems for sequences spaces. Pacific J. Math. 46 (1973), 17–30.CrossRefGoogle Scholar
[2]Bessaga, C. and Pelczynski, A.. On bases and unconditional convergence of series in Banach spaces. Studia Math. 17 (1958), 151–164.CrossRefGoogle Scholar
[3]Kuttner, B.. Note on strong summability. J. London Math. Soc. 21 (1946), 118–122.Google Scholar
[4]Lascarides, C. G. and Maddox, I. J.. Matrix transformations between some classes of sequences. Math. Proc. Cambridge Philos. Soc. 68 (1970), 99–104.CrossRefGoogle Scholar
[5]Maddox, I. J.. On Kuttner's theorem. J. London Math. Soc. 43 (1968), 285–290.CrossRefGoogle Scholar
[6]Maddox, I. J. and Willey, M. A. L.. Continuous operators on paranormed spaces and matrix transformations. Pacific J. Math. 53 (1974), 217–228.CrossRefGoogle Scholar
[7]Maddox, I. J.. FK spaces which include strongly summable sequences. Math. Proc. Cambridge Philos. Soc. 93 (1983), 131–134.CrossRefGoogle Scholar
[8]McArthur, C. W. and Retherford, J. R.. Some applications of an inequality in locally convex spaces. Trans. Amer. Math. Soc. 137 (1969), 115–123.CrossRefGoogle Scholar
[9]Simons, S.. The sequence spaces l (pv) and m(p v). Proc. London Math. Soc. (3) 15 (1965), 422–436.CrossRefGoogle Scholar
[10]Singer, I.. Some remarks on domination of sequences. Math. Ann. 184 (1970), 113–132.CrossRefGoogle Scholar
[11]Thorpe, B.. An extension of Kuttner's theorem. Bull. London Math. Soc. 13 (1981), 301–302.CrossRefGoogle Scholar
[12]Zeller, K.. Allgemeine Eigenschaften von Limitierungsverfahren. Math. Z. 53 (1951), 463–487.CrossRefGoogle Scholar