In this paper we shall prove the following two results.

Theorem 1. Let ∊ > 0 and β a real number be given. Them, for almost all real a (in the sense of Lebesque measure), there are infinitely many pairs of square-free integers m, n such that

In this article an estimate is obtained for the coefficients of the transformation polynomials for the elliptic modular function. This enables us to answer some questions raised by Mahler in [5] and [6].

The main purpose of this paper is to classify the maximal p-local subgroups of the Lyons group Ly, of order 51,765,179,004,000,000 = 28.37.56.7.11.31.37.67, for each primes dividing the order of the group. We also determine which of these are maximal subgroups of Ly, and in Sections 5 and 6 we give some information on the non-local subgroups.

Bieri and Strebel [2] have established a striking criterion that determines whether a metabelian group is finitely presented. This criterion is of a sort that implies that all homomorphic images of a finitely presented metabelian group are finitely presented. Another of their results is that the class of nilpotent-of-class-two-by-abelian groups has the property that all homomorphic images of finitely presented groups in this class are finitely presented. However, they point out that an example due to Abels [1] shows that the class of nilpotent-of-class-three-by-abelian groups does not have this property. One could not therefore expect that a criterion of the same type as that of Bieri and Strebel would distinguish the finitely presented groups in general classes of nilpotent-by-abelian groups. One might hope, however, to find such a criterion for nilpotent-of-class-two-by-abelian groups. The aim of this paper is to make some steps in this direction, by finding a sufficient condition for such groups to be finitely presented.

The following concept of (not necessarily commutative) Noetherian unique factorization domain (UFD) was introduced recently by A. W. Chatters. Recall that an ideal P of a ring R is called completely prime if R/P is a domain. The element p∊R will be called a prime element if pR =Rp is a completely prime, height one prime of R. C(P) denotes the set of elements of R which are regular modulo P. Set C = ∩ C(P) where P ranges over the height one primes of R.

In the theory of locales (or ‘pointless topology’), approximations to the Alexandrov-Hopf separation axioms have been considered by several authors [2,4,9,…]. The T1 axiom has proved more recalcitrant than the others; as yet, no-one has found a satisfactory lattice-theoretic condition of roughly the same strength.

The object of this paper is to generalize the relative Mayer-Vietoris sequence of Eilenberg and Steenrod([3], p. 42) by allowing both the containing spaces and the subspaces to vary. Fix a generalized homology theory h*. We call a couple of spaces {X1, X2} excisive (for h*) if they are subspaces of some larger space and the inclusion (X1, X1 ∩ X2) → (X1 ∪ X2, X2) induces an isomorphism under h* (see [4], pp. 208–9 for equivalent definitions).

The mod two homology of MSpin, the Spin-cobordism Thom spectrum, has a rich algebraic structure. We will describe it explicitly as a comodule algebra, and give some applications to the ring structure of the Spin-cobordism ring.

Let A = {Aq}q≥0 be an anti-commutative graded ring with 1. Let X be a space and let G(X; A) be the group of multiplicative units of the ring Πi≥0Hi(X; Ai) of the form l + x1 + x2 +…, where xi∊ Hi (X; Ai), In [6] Segal showed that there is a connective cohomology theory G*(X; A), with G0(X;A) = G(X; A). This was improved by Steiner, who in [7] showed that A→G*(X; A) is a functor from anticommutative graded algebras to cohomology theories.

The technique of introducing singularities of some form to a bordism theory proposed in [7] by Sullivan and developed in [1] has proved itself to be a very efficient method of constructing new homology and cohomology theories with predetermined properties (see, for example [3]–[6]). We propose a generalization of this method taking as our starting point a complex of free U*-modules endowed with an additional ‘geometric’ structure. The Sullivan—Baas construction of killing a regular sequence x1, x2, … of elements of U* fits in our framework as a special case of Koszul resolution of U*/(x1, x2, …) with some canonical structure. Also, when specialized to the U*-complex of the form U* ⊗Z C for a ℤ-complex of length 3, our construction turns out to be equivalent to the ‘bordisms with coefficients’ described in [2].

The purpose of this paper is to establish an embedding of QM (A), the Banach space of all quasi-multipliers on A, in the second conjugate space A** of a Banach algebra A, which extends the well-known embedding of the left multipliers (right multipliers) of A in A**. We also prove that, for a dual B*-algebra, QM(A) is isometrically isomorphic to A**.

Singer [10] defined a series Σxk in a Banach space X to be weakly p-unconditionally Cauchy if and only if Σλkxk converges in X for all λ∊lp, where 1 < p < ∞. For Banach spaces containing no subspace isomorphic to c0 Singer characterized such series as those for which

where 1/p + 1/q = 1 and X′ is the dual space of X.

Let X1, …, Xn be independent Bernoulli random variables, and let pi = P[Xi = 1], λ = Σi=1n pi and Σi=1n Xi. Successively improved estimates of the total variation distance between the distribution ℒ(W) of W and a Poisson distribution Pλ with mean λ have been obtained by Prohorov[5], Le Cam [4], Kerstan[3], Vervaat[8], Chen [2], Serfling[7] and Romanowska[6]. Prohorov, Vervaat and Romanowska discussed only the case of identically distributed Xi's, whereas Chen and Serfling were primarily interested in more general, dependent sequences. Under the present hypotheses, the following inequalities, here expressed in terms of the total variation distance

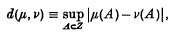
were established respectively by Le Cam, Kerstan and Chen:

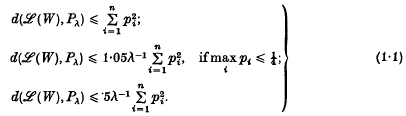
(Kerstan's published estimate of 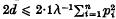([3], p.174, equation (1)) is a misprint for 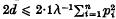, the constant 2·1 appearing twice on p. 175 of his paper.) Here, we use Chen's [2] elegant adaptation of Stein's method to improve hte estimates given in (1·1), and we complement these estimates with a reverse inequality expressed in similar terms. Second order estimates, and the case of more general non-negative integer valued X's, are also discussed.

For elastic or plastic media the linkages between basic properties at two levels of description are rigorously analysed. At one level the material is structurally heterogeneous, while at the other it behaves macroscopically as if homogeneous. The deformation is unrestricted as to magnitude, but is treated incrementally. Full account is taken of coupling between stresses and rotations within a representative volume. Theorems on spatial averages of tensor variables and their products are reviewed and extended. Relations between constitutively significant quantities at both levels are developed by means of tensor influence functions associated with auxiliary elastic fields. The analysis is conducted primarily in terms of non-objective variables and a Lagrangian reference configuration. A final transformation to intrinsic variables is effected with the help of some novel operators.

Two, essentially different, criteria for truncating a potential function of a conservative structural system are reviewed, one based on deflection considerations and the other on the mathematical concept of determinacy. Formulations in which they give different results are discussed; most importantly, these include Koiter's 1976 form for mode interaction in stiffened structure [11], which exhibits Thorn's parabolic umbilic catastrophe [15]. For this case, two alternative schemes of perturbation analysis are presented, each describing asymptotically the post-buckling response. The more obvious approach turns out to be the less successful, being linked to an indeterminate, too severely truncated, form of the potential function.

The second, determinacy linked, approach generates as a first-order response a distinctive looping pattern of equilibrium paths, which has recently been identified in a simple model due to Budiansky and Hutchinson[1], by exact, closed-form, solution [8]. The convergence of each asymptotic scheme to the exact solution is briefly reviewed for this simple model, by plotting first and second order results.

Lemma 4·1, which appears on p. 289 of [2], is false. Nevertheless, Theorem 4·2, the only result dependent upon it, is true. The following supplies the necessary modification to the proof.

Volume 92 (1982), 115–119

K. J. Falconer

School of Mathematics, University of Bristol

‘Growth conditions on powers of Hermitian elements’

The above paper aimed to obtain Banach algebra equivalents of the elegant theorems of Roe [2] and Burkill [1] which gave characterizations of the sine function. Professor John Duncan has kindly pointed out that the paper contains two oversights, with the result that the theorems stated are not the strict Banach algebra equivalents as was claimed. (The assertion on p. 117 that T is Hermitian is false if μ > 0, and at the bottom of p. 117 it follows from Theorem 2 that F0(t) = c1eit + c2eit so that a2 – e = 0.) Whilst Theorems 1–3 are correct as stated, the conclusions of Theorems 1 and 3 must be strengthened to provide equivalent versions when μ > 0. In the basic case when μ = 0, the analysis remains as given.