Hostname: page-component-78c5997874-mlc7c Total loading time: 0 Render date: 2024-11-09T09:20:33.801Z Has data issue: false hasContentIssue false
  • English
  • Français

The roots of Yn(λη)Jn(λ) – Jn(λη) Yn(λ) = 0

Published online by Cambridge University Press:  24 October 2008

S. Chandrasekhar  and
Donna Elbert
S. Chandrasekhar
Affiliation:
The Yerkes ObservatoryUniversity of Chicago
Donna Elbert
Affiliation:
The Yerkes ObservatoryUniversity of Chicago
Get access Rights & Permissions [Opens in a new window]

Extract

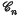Cylinder functions, (λx), of integral orders which vanish at x = 1 and x = η (where η is an assigned positive constant less than 1) occur in the solution of many problems in applied mathematics. Such functions can be expressed in terms of the Bessel functions Jn(x) and Yn(x) of the two kinds in the form

where λ is a root of the equation

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 50 , Issue 2 , April 1954 , pp. 266 - 268
Copyright
Copyright © Cambridge Philosophical Society 1954

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1) British Association Mathematical Tables, vol. 10. Bessel functions: functions of positive integral order (Cambridge, 1952).Google Scholar
(2)Carslaw, H. S. and Jaeger, J. C.Conduction of heat in solids (Oxford, 1947), Appendix IV, Table IV, p. 379.Google Scholar
(3)Chandrasekhar, S.Journal of Rational Mechanics and Analysis. (In the Press.)Google Scholar
(4)Chandrasekhar, S. and Elbert, D.Proc. Camb. phil. Soc. 49 (1953), 446.Google Scholar
(5)Gray, A. and Mathews, G. B.A treatise on Beseel functions, 2nd ed. (London, 1922), p. 82.Google Scholar
(6)Lowan, A. N. and Hillman, A.J. Math. Phys. 22 (1943), 208.CrossRefGoogle Scholar
(7)Reinstein, E. Untersuchungen über die Transversal-schwingungen (Göttingen Dissertation: Leipzig) (1911).Google Scholar