Hostname: page-component-586b7cd67f-dlnhk Total loading time: 0 Render date: 2024-11-29T18:54:23.839Z Has data issue: false hasContentIssue false
  • English
  • Français

Recurrence and transience of reflecting Brownian motion in the quadrant

Published online by Cambridge University Press:  24 October 2008

D. G. Hobson  and
L. C. G. ROGERS
D. G. Hobson
Affiliation:
Statistical Laboratory, University of Cambridge, 16 Mill Lane, Cambridge, CB2 1SB
L. C. G. ROGERS
Affiliation:
School of Mathematical Sciences, Queen Mary and Westfield College, University of London, Mile End Road, London, E1 4NS
Get access Rights & Permissions [Opens in a new window]

Extract

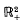In this paper we obtain criteria for a reflecting Brownian motion in the first orthant of the plane to reach an arbitrary open neighbourhood of the origin in finite time, or in finite mean time. The reflecting Brownian motion (RBM) is assumed to have a constant non-zero drift, and a constant non-singular covariance, and the directions of reflection on the two sides of 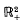are constant along each side, but not necessarily normal. We explain why the criteria we find are to be expected.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 113 , Issue 2 , March 1993 , pp. 387 - 399
Copyright
Copyright © Cambridge Philosophical Society 1993

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Bingham, N. H.. Fluctuation theory in continuous time. Adv. in Appl. Probab. 7 (1975), 705–766.CrossRefGoogle Scholar
[2]Foster, F. G.. On the stochastic matrices associated with certain queuing processes. Ann. Math. Statist. 24 (1953), 355–360.CrossRefGoogle Scholar
[3]Fristedt, B.. Sample functions of stochastic processes with stationary independent increments. Adv. in Appl. Probab. 3 (1973), 241–396.Google Scholar
[4]Harrison, J. M. and Reiman, M. I.. Reflected Brownian motion on an orthant. Ann. Probab. 9 (1981), 302–308.CrossRefGoogle Scholar
[5]Harrison, J. M. and Williams, R. J.. Brownian models of open queuing networks with homogeneous customer populations. Stochastics 22 (1987), 77–115.CrossRefGoogle Scholar
[6]Harrison, J. M. and Williams, R. J.. Multidimensional reflected Brownian motions having exponential stationary distributions. Ann. Probab. 15 (1987), 115–137.CrossRefGoogle Scholar
[7]Kingman, J. F. C.. The ergodic behaviour of random walks. Biometrika 48 (1961), 391–396.CrossRefGoogle Scholar
[8]Lions, P. L. and Snitzman, A. S.. Stochastic differential equations with reflecting boundary conditions. Comm. Pure Appl. Math. 37 (1987), 511–537.CrossRefGoogle Scholar
[9]Malyšev, V. A.. Classification of two-dimensional positive random walks and almost linear semi-martingales. Soviet Math. Dokl. 13 (1972), 136–139.Google Scholar
[10]Rogers, L. C. G.. A new identity for real Lévy processes. Ann. lnst. Henri Poincaré Probab. Statist. 20 (1984), 21–34.Google Scholar
[11]Rogers, L. C. G.. A guided tour through excursions. Bull. London Math. Soc. 21 (1989), 305–341.CrossRefGoogle Scholar
[12]Rosenkrantz, W. A., Ergodicity conditions for two-dimensional Markov chains on the positive quadrant. Probab. Theory Belated Fields 83 (1989), 309–319.CrossRefGoogle Scholar
[13]Silverstein, M. L.. Classification of coharmonic and coinvariant functions for a Lévy process. Ann. Probab. 8 (1980), 539–575.CrossRefGoogle Scholar
[14]Varadhan, S. R. S. and Williams, R. J.. Brownian motion in a wedge with oblique reflection. Comm. Pure Appl. Math. 38 (1985), 405–443.CrossRefGoogle Scholar
[15]Williams, R. J.. Recurrence classification and invariant measure for reflected Brownian motion in a wedge. Ann. Probab. 13 (1985), 758–778.CrossRefGoogle Scholar