Hostname: page-component-78c5997874-v9fdk Total loading time: 0 Render date: 2024-11-06T05:05:07.217Z Has data issue: false hasContentIssue false
  • English
  • Français

Quadratic Lyapunov functions for linear systems

Published online by Cambridge University Press:  24 October 2008

Y. V. Venkatesh
Y. V. Venkatesh
Affiliation:
Department of Electrical Engineering, Indian Institute of Science, Bangalore 12, India
Get access Rights & Permissions [Opens in a new window]

Abstract

The paper deals with the existence of a quadratic Lyapunov function V = x′P(t)x for an exponentially stable linear system with varying coefficients described by the vector differential equation 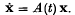The derivative dV/dt is allowed to be strictly semi-(F) and the locus dV/dt = 0 does not contain any arc of the system trajectory. It is then shown that the coefficient matrix A(t) of the exponentially stable system is not identically equal to a unit matrix multiplied by a scalar. The result subsumes that of Lehnigk(1).

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 66 , Issue 1 , July 1969 , pp. 115 - 117
Copyright
Copyright © Cambridge Philosophical Society 1969

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Lehnigk, S. H.Quadratic forms as Liapunov functions for linear differential equations with real constant coefficients. Proc. Cambridge Philos. Soc. 61 (1965), 883–888.CrossRefGoogle Scholar
(2)Malkin, I. G.On the construction of Lyapunov functions for systems of linear equations. Prikl. Mat. Meh. 16 (1952), 239–242.Google Scholar
(3)Coddington, B. A. and Levinson, N.Theory of ordinary differential equations (McGraw Hill; New York, 1955).Google Scholar
(4)Hahn, W.Theory and applications of Lyapunov's direct method (Prentice-Hall, Englewood Cliffs; N.J. 1963).Google Scholar