Hostname: page-component-78c5997874-m6dg7 Total loading time: 0 Render date: 2024-11-19T17:50:30.821Z Has data issue: false hasContentIssue false
  • English
  • Français

Quadratic forms between spheres and the non-existence of sums of squares formulae

Published online by Cambridge University Press:  24 October 2008

Paul Y. H. Yiu
Paul Y. H. Yiu
Affiliation:
Department of Mathematics, University of British Columbia, Vancouver, B.C. V6T 1Y4, Canada
Get access Rights & Permissions [Opens in a new window]

Extract

Hurwitz [6] posed in 1898 the problem of determining, for given integers r and s, the least integer n, denoted by r s, for which there exists an [r, s, n] formula, namely a sums of squares formula of the type

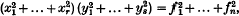
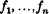where are bilinear forms with real coefficients in 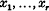and 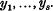. Such an 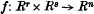[r, s, n] formula is equivalent to a normed bilinear map satisfying 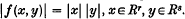. We shall, therefore, speak of sums of squares formulae and normed bilinear maps interchangeably.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 100 , Issue 3 , November 1986 , pp. 493 - 504
Copyright
Copyright © Cambridge Philosophical Society 1986

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Adams, J. F.. On the nonexistence of elements of Hopf invariant one. Ann. of Math. 72 (1960), 20–104.CrossRefGoogle Scholar
[2]Adem, J.. Construction of some normed maps. Bol. Soc. Mat. Mexicana 20 (1975), 59–75.Google Scholar
[3]Al-Sabti, G. and Bier, T.. Elements in the stable homotopy groups of spheres which are not bilinearly representable, Bull. London Math. Soc. 10 (1978), 197–200.CrossRefGoogle Scholar
[4]Eells, J. and Lemaire, L.. Selected topics in harmonic maps. Regional Conference Series in Mathematics,no. 50(1983).CrossRefGoogle Scholar
[5]Hopf, H.. Ein topologischer Beitrag zur reellen Algebra. Comment. Math. Helv. 13 (1941), 219–239.CrossRefGoogle Scholar
[6]Hurwitz, A.. Über die Komposition der quadratischen Formen von beliebig vielen Variablen. Nach. v. der Ges. der Wiss., Göttingen (Math. Phys. KI.) (1898), 309–316; reprinted in Math. Werke, Bd. 2, pp. 565–571.Google Scholar
[7]Hurwitz, A.. Über die Komposition der quadratischen Formen. Math. Ann. 88 (1923), 1–25; reprinted in Math. Werke Bd. 2, pp. 641–666.CrossRefGoogle Scholar
[8]Lam, K. Y.. Construction of nonsingular bilinear maps. Topology 6 (1967), 423–426.CrossRefGoogle Scholar
[9]Lam, K. Y.. A note on Stiefel manifolds and the generalized J homomorphism. Bol. Soc. Mat. Mexicana 21 (1976), 33–38.Google Scholar
[10]Lam, K. Y.. Nonsingular bilinear maps, and stable homotopy classes of spheres. Math. Proc. Cambridge Philos. Soc. 82 (1977), 419–425.CrossRefGoogle Scholar
[11]Lam, K. Y.. Topological methods for studying the composition of quadratic forms. Canadian Math. Soc. Conf. Proc. 4 (1984), 173–192.Google Scholar
[12]Lam, K. Y.. Some new results in composition of quadratic forms. Invent. Math. 79 (1985), 467–474.CrossRefGoogle Scholar
[13]Milgram, R. J.. Immersing protective spaces. Ann. Math. 85 (1967), 473–482.CrossRefGoogle Scholar
[14]Milgram, R. J., Strutt, J. and Zvengrowski, P.. Projective stable stems of spheres. Bol. Soc. Mat. Mexicana 22 (1977), 48–57.Google Scholar
[15]Paechter, G. F.. The groups . Quart. J. Math. Oxford 7 (1956), 249–268.CrossRefGoogle Scholar
[16]Radon, J.. Lineare Scharen orthogonalen Matrizen. Abh. Math. Sem. Univ. Hamburg 1 (1922), 1–14.CrossRefGoogle Scholar
[17]Roitberg, J.. Dilatation phenomena in the homotopy groups of spheres. Advances in Math. 15 (1975), 198–206.CrossRefGoogle Scholar
[18]Shapiro, D. B.. Products of sums of squares. Expo. Math. 2 (1984), 235–261.Google Scholar
[19]Stiefel, E.. Üjer Richtungsfelder in den projektiven Raumen und einen Satz aus reellen Algebra. Comment. Math. Helv. 13 (1941), 201–218.CrossRefGoogle Scholar
[20]Wong, Y. C.. Isoclinic n-planes in euclidean 2n-spaee, Clifford Parallels in elliptic (2n−1)-space, and the Hurwitz Matrix Equations. Mem. Amer. Math. Soc. 41 (1961).Google Scholar
[21]Wood, R.. Polynomial maps from spheres to spheres. Invent. Math. 5 (1968), 163–168.CrossRefGoogle Scholar
[22]Yiu, P.. Sums of squares formulae with integer coefficients. Preprint.Google Scholar
[23]Yuzvinsky, S.. Orthogonal pairings of euclidean spaces. Michigan Math. J. 28 (1981), 131–145.CrossRefGoogle Scholar
[24]Yuzvinsky, S.. A series of monomial pairings. Linear and Multilinear Algebra 15 (1984), 109–119.CrossRefGoogle Scholar