Hostname: page-component-586b7cd67f-t7czq Total loading time: 0 Render date: 2024-11-26T13:17:57.590Z Has data issue: false hasContentIssue false
  • English
  • Français

Orientable surfaces in the 4-sphere associated with non-orientable knotted surfaces

Published online by Cambridge University Press:  24 October 2008

Seiichi Kamada
Seiichi Kamada
Affiliation:
Department of Mathematics, Osaka City University, Osaka, 558, Japan
Get access Rights & Permissions [Opens in a new window]

Extract

Let F be a closed connected and non-orientable surface smoothly embedded in the 4-sphere S4 with normal Euler number e(F) = 0. We note that if e(F) = 0, then the non-orientable genus n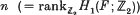 is even (ef. [7]) and the tubular neighbourhood N(F) of F in S4 which is a D2-bundle over F has a trivial I-subbundle. Let τ be a trivial I-subbundle of N(F) and let τ* = F × I ⊂ N(F) be its orthogonal I-subbundle which is twisted. Then 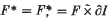is a closed connected genus n – 1 orientable surface smoothly embedded in S4 and doubly covers F. We call this surface a doubled surface of F in S4 (associated with τ). If a trivial I-subbundle τ is given, then we see that the knot type of F* ⊂ S4 is uniquely determined.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 108 , Issue 2 , September 1990 , pp. 299 - 306
Copyright
Copyright © Cambridge Philosophical Society 1990

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Asano, K.. A note on surfaces in 4-spheres. Math. Sem. Notes Kobe Univ. 4 (1976), 195–198.Google Scholar
[2]Hosokawa, F. and Kawauchi, A.. Proposal for unknotted surfaces in four-space. Osaka J. Math. 16 (1979), 233–248.Google Scholar
[3]Kamada, S.. On doubled surfaces of nonorientablė surfaces in the 4-sphere. Kobe J. Math. (To appear.)Google Scholar
[4]Kawauchi, A.. Three dualities on the integral homology of infinite cyclic coverings of manifolds. Osaka J. Math. 23 (1986), 633–651.Google Scholar
[5]Levine, J.. Polynomial invariants of knots of codimension two. Ann. of Math. 84 (1966), 537–554.CrossRefGoogle Scholar
[6]Litherland, R. A.. The second homology of the group of a knotted surface. Quart. J. Math. Oxford Ser. (2) 32 (1981), 425–434.CrossRefGoogle Scholar
[7]Massey, W. S.. Proof of a conjecture of Whitney. Pacific J. Math. 31 (1969), 143–156.CrossRefGoogle Scholar