On the summation of certain trigonometric series
Published online by Cambridge University Press: 24 October 2008
Extract
In the present note, which is introductory to the following paper, closed expressions, suitable for computational purposes, are found for the sums of the series
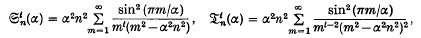
where α > 1, t = 1, 2, 3, …, and n is a positive integer. In each case a recurrent relation is found giving the values of 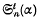 and
and 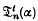 for t > 2 in terms of
for t > 2 in terms of 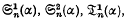
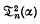 and the series Θκ(α) (κ = 1, 2, …, t), where
and the series Θκ(α) (κ = 1, 2, …, t), where
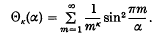
When κ is even the last series is expressed in closed form in terms of the Bernoullian polynomial φκ(l/α) and, when κ is odd and α is rational, a closed form is found involving the polygamma function Ψ(κ)(z), where 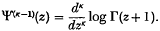 The general expressions for
The general expressions for 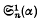 and
and 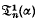 involve Ψ(z) and Ψ′(z) when α is rational, but for special values of α they reduce to a form independent of the Ψ-function.
involve Ψ(z) and Ψ′(z) when α is rational, but for special values of α they reduce to a form independent of the Ψ-function. 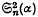 and
and 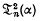 are independent of n and are expressible as simple rational functions of α.
are independent of n and are expressible as simple rational functions of α.
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 41 , Issue 2 , June 1945 , pp. 145 - 160
- Copyright
- Copyright © Cambridge Philosophical Society 1945
References
REFERENCES
- 3
- Cited by


