Research Article
The minima of a pair of indefinite, harmonic, binary quadratic forms
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 77-96
-
- Article
- Export citation
Totally heterogeneous continua
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 96-103
-
- Article
- Export citation
A general form of the covering principle and relative differentiation of additive functions
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 103-110
-
- Article
- Export citation
On multiple curves. I
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 111-117
-
- Article
- Export citation
On multiple curves. II
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 117-126
-
- Article
- Export citation
Covariant line complexes of a pair of quadric surfaces
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 127-135
-
- Article
- Export citation
Point-curve correspondences: I. The theory of the base
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 135-145
-
- Article
- Export citation
On the summation of certain trigonometric series
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 145-160
-
- Article
- Export citation
A method for computing the resonant wave-length of a type of cavity resonator
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 160-175
-
- Article
- Export citation
The quantum mechanics of a bounded linear harmonic oscillator
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 175-179
-
- Article
- Export citation
The energy levels of ‘holes’ in liquids
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 180-183
-
- Article
- Export citation
Research Note
On the classical theory of radiating electrons
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 184-186
-
- Article
- Export citation
Front matter
PSP volume 41 issue 2 Cover and Front matter
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back matter
PSP volume 41 issue 2 Cover and Back matter
-
- Published online by Cambridge University Press:
- 24 October 2008, p. b1
-
- Article
-
- You have access
- Export citation

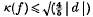 and that this is a ‘best possible’ result.
and that this is a ‘best possible’ result.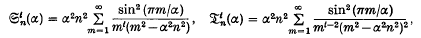
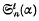 and
and 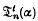 for
for 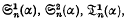
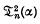 and the series Θ
and the series Θ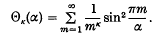
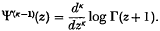 The general expressions for
The general expressions for 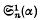 and
and 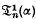 involve Ψ(
involve Ψ(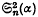 and
and 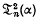 are independent of
are independent of 
 , and the external electromagnetic field is described by the usual field quantities
, and the external electromagnetic field is described by the usual field quantities