Hostname: page-component-586b7cd67f-dsjbd Total loading time: 0 Render date: 2024-11-26T07:33:36.416Z Has data issue: false hasContentIssue false
  • English
  • Français

On the stability of the set of hyperbolic closed orbits of a Hamiltonian

Published online by Cambridge University Press:  03 June 2010

MÁRIO BESSA ,
CÉLIA FERREIRA  and
JORGE ROCHA
MÁRIO BESSA
Affiliation:
Departamento de Matemática, Universidade do Porto, Rua do Campo Alegre, 687, 4169-007 Porto, Portugal. ESTGOH-Instituto Politécnico de Coimbra, Rua General Santos Costa, 3400-124 Oliveira do Hospital, Portugal. e-mail: [email protected]
CÉLIA FERREIRA
Affiliation:
Departamento de Matemática, Universidade do Porto, Rua do Campo Alegre, 687, 4169-007 Porto, Portugal. e-mail: [email protected], [email protected]
JORGE ROCHA
Affiliation:
Departamento de Matemática, Universidade do Porto, Rua do Campo Alegre, 687, 4169-007 Porto, Portugal. e-mail: [email protected], [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Let H be a Hamiltonian, e ∈ H(M) ⊂ ℝ and ƐH, e a connected component of H−1({e}) without singularities. A Hamiltonian system, say a triple (H, e, ƐH, e), is Anosov if ƐH, e is uniformly hyperbolic. The Hamiltonian system (H, e, ƐH, e) is a Hamiltonian star system if all the closed orbits of ƐH, e are hyperbolic and the same holds for a connected component of 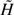−1({ẽ}), close to ƐH, e, for any Hamiltonian 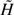, in some C2-neighbourhood of H, and ẽ in some neighbourhood of e.

In this paper we show that a Hamiltonian star system, defined on a four-dimensional symplectic manifold, is Anosov. We also prove the stability conjecture for Hamiltonian systems on a four-dimensional symplectic manifold. Moreover, we prove the openness and the structural stability of Anosov Hamiltonian systems defined on a 2d-dimensional manifold, d ≥ 2.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 149 , Issue 2 , September 2010 , pp. 373 - 383
Copyright
Copyright © Cambridge Philosophical Society 2010

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Andronov, A. and Pontrjagin, L.Systèmes grossiers. Dokl. Akad. Nauk. SSSR. 14 (1937), 247–251.Google Scholar
[2]Anosov, D. V.Geodesic flows on closed Riemannian manifolds of negative curvature. Proc. Steklov Math. Inst. 90 (1967), 1–235.Google Scholar
[3]Aoki, N.The set of Axiom A diffeomorphisms with no cycles. Bol. Soc. Brasil. Mat. (N.S.). 23, 1–2 (1992), 21–65.CrossRefGoogle Scholar
[4]Arnaud, M.-C.Un lemme de fermeture d'orbites: le “orbit closing lemma”. [An orbit closing lemma]. C. R. Acad. Sci. Paris Sér. I Math. 323, 11 (1996), 1175–1178.Google Scholar
[5]Bessa, M. and Lopes Dias, J.Generic dynamics of 4-dimensional C 2 hamiltonian systems. Commun. Math. Phys. 281 (2008), 597–619.CrossRefGoogle Scholar
[6]Bessa, M. and Lopes Dias, J.Hamiltonian elliptic dynamics on symplectic 4-manifolds. Proc. Amer. Math. Soc. 137 (2009), 585–592.CrossRefGoogle Scholar
[7]Bessa, M. and Rocha, J.Three-dimensional conservative star flows are Anosov. Disc. Cont. Dynam. Sys. A. 26, 3 (2010), 839–846.CrossRefGoogle Scholar
[8]Brin, M. and Stuck, G.Introduction to dynamical systems. (Cambridge University Press, 2002).CrossRefGoogle Scholar
[9]Doering, C.Persistently transitive vector fields on three-dimensional manifolds. Proc. Dynam. Sys. Bifurc. Th. Pitman Res. Notes in Math. 160 (1987), 59–89.Google Scholar
[10]Gan, S. and Wen, L.Nonsingular star flows satisfy Axiom A and the no-cycle condition. Invent. Math. 164 (2006), 279–315.CrossRefGoogle Scholar
[11]Hayashi, S.Diffeomorphisms in F 1(M) satisfy Axiom A. Ergod. Th. Dynam. Sys. 12, 2 (1992), 233–253.CrossRefGoogle Scholar
[12]Hirsch, M. W., Pugh, C.C. and Shub, M.Invariant manifolds. Lecture Notes in Mathematics, 583 (Springer-Verlag, 1977).CrossRefGoogle Scholar
[13]Hurewicz, W. and Wallman, H.Dimension Theory. Princeton Mathematical Series, 4 (Princeton University Press, 1941).Google Scholar
[14]Katok, A. and Hasselblatt, B.Introduction to the Modern Theory of Dynamical Systems, (Cambridge University Press, 1995).CrossRefGoogle Scholar
[15]Mañé, R.A proof of the C 1 stability conjecture. Inst. Hautes Études Sci. Publ. Math. 66 (1988), 161–210.CrossRefGoogle Scholar
[16]Mañé, R.An ergodic closing lemma. Ann. of Math. 116, 3 (1982), 503–540.CrossRefGoogle Scholar
[17]Oseledets, V. I.A multiplicative ergodic theorem: Lyapunov characteristic number for dynamical systems. Trans. Moscow Math. Soc. 19 (1968), 197–231.Google Scholar
[18]Pugh, C. and Robinson, C.The C 1 closing lemma, including Hamiltonians. Ergod. Th Dynam. Sys. 3 (1983), 261–313.CrossRefGoogle Scholar
[19]Robinson, C.Lectures on Hamiltonian Systems. Monografias de Matemática (IMPA, 1971).Google Scholar
[20]Shub, M.Global Stability of Dynamical Systems (Springer-Verlag, 1987).CrossRefGoogle Scholar
[21]Tucker, W.The Lorenz attractor exists. C. R. Acad. Sci. Paris Sér. I Math. 328, 12 (1999), 1197–1202.CrossRefGoogle Scholar
[22]Vivier, T. Robustly transitive 3-dimensional regular energy surfaces are Anosov. Institut de Mathématiques de Bourgogne, Dijon, Preprint 412 (2005). http://math.u-bourgogne.fr/topo/prepub/pre05.html.Google Scholar