Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-24T02:47:09.307Z Has data issue: false hasContentIssue false
  • English
  • Français

On non-linear differential equations of the second order

III. The equation ẍ − k(1 − x2)ẋ + x = p.kλ cos (λt + α), k small and λ near 1.

Published online by Cambridge University Press:  24 October 2008

M. L. Cartwright
M. L. Cartwright
Affiliation:
Girton CollegeCambridge
Get access Rights & Permissions [Opens in a new window]

Extract

1. The problem of automatic synchronization of triode oscillators was studied by Appleton† and van der Pol‡; it gives rise to the differential equation

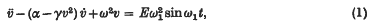
where α, γ, ω, E, ω1 are positive constants such that α/ω, γ/ω, (ω − ω1)/ω are small and dots denote differentiations with respect to t. When these conditions are satisfied, it is easy to see that

is an approximate solution over a limited time for any b1, b2 chosen to fit initial conditions on v and ṿ provided that v and ṿ are not too large. If it is assumed that b1 and b2 vary slowly compared with ω1t, so that 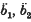can be neglected, and ḃ1, ḃ2 are comparatively small, the equations

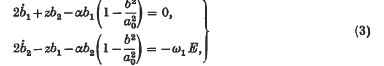
where

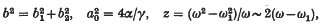
are obtained. These are sufficiently accurate for the discussion of most of the physical phenomena, and have been used in this form (or in the polar-coordinate form obtained by putting b1 = b cos ø, b2 = b sin ø) by various authors §. Solutions of (1) with period 2π/ω1 are obtained approximately by putting ḃ1 = ḃ2 = 0 in (3). The steady-state solutions of (1) other than those with period 2π/ω1 correspond to periodic solutions of (3). All other solutions converge to one or other of these types of solution.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 45 , Issue 4 , October 1949 , pp. 495 - 501
Copyright
Copyright © Cambridge Philosophical Society 1949

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

† Appleton, E. V., Proc. Cambridge Phil. Soc. 21 (1922), 231–48.Google Scholar

‡ van der Pol, B., Phil. Mag. 3 (1927), 65–80.CrossRefGoogle Scholar This gives references to earlier work.

§ See Cartwright, M. L., J. Instn Elect. Engrs, 95, Part iii (1948), 88–96.Google Scholar This gives further references.

∥ See, for instance, Mandelstam, L., Papalexi, N., Andronov, A., Chaikin, S. and Witt, A., Technical Physics of the U.S.S.R. 2 (1935) (in French), 81–134Google Scholar (90), which indicates a method based on Fatou, P., Bull. Soc. Math. France, 56 (1928), 98–139.Google Scholar See also N. Kryloff and N. Bogoliuboff, ‘Méthodes de la mécanique non linéaires appliquées à l'étude des oscillations stationnaires’ (Monograph in Russian with summary in French, Kiev, 1934), Ukrainska Akad. Nauk, Inst. Mecanique, Report no. 8, pp. 1–112.Google Scholar

† Cartwright, M. L., J. Instn Elect. Engrs, 95, Part iii, 88–96Google Scholar with 2E 1 = p.

‡ See Cartwright, M. L. and Littlewood, J. E., Ann. Math. 48 (1947), 472–94.CrossRefGoogle Scholar

† I have to thank the referee for pointing this out, and so enabling me to omit a large part of the proof.

‡ See Kamke, E., Differentialgleichungen reeller Funktionen (Leipzig, 1930), p. 93.Google Scholar

† Compare Bieberbach, L., Differentialgleichungen (Berlin, 1930), pp. 74–8;Google Scholar also Levinson, N., Ann. Math. 45 (1944), 723–37,CrossRefGoogle Scholar and Hadamard, J., Bull. Soc. Math. France, 26 (1901).Google Scholar

† Levinson calls this a directly unstable point. A discussion of the various cases which occur for equations (5) will be found in Cartwright, M. L., J. Instn Elect. Engrs, 95, part iii (1948), 88–96.Google Scholar There are certain other cases which cannot occur for equations (5) and (20).

‡ See Rouché's theorem, Alexandroff, P. and Hopf, H., Topologie, 1 (Berlin, 1935), 459.Google Scholar

§ We use stars to denote parameters, functions, etc., defined with reference to the exactly periodic solution determined by but the strict correspondence between starred and unstarred letters necessarily breaks down in the case of the various functions involved.

† Compare Alexandroff, P. A. and Hopf, H., Topologie, 1 (Berlin, 1930), 458Google Scholar et seq.

‡ See, for instance, Levinson, N., Ann. Math. 45 (1944), 723–37CrossRefGoogle Scholar or Cartwright, M. L., Research, 1 (1948).Google Scholar