Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Warren, Audie
2019.
On products of shifts in arbitrary fields.
Moscow Journal of Combinatorics and Number Theory,
Vol. 8,
Issue. 3,
p.
247.
Pham, Thang
and
Vinh, Lê Anh
2020.
Distribution of distances in positive characteristic.
Pacific Journal of Mathematics,
Vol. 309,
Issue. 2,
p.
437.
Hase-Liu, Matthew
and
Sheffer, Adam
2020.
Sum–product phenomena for planar hypercomplex numbers.
European Journal of Combinatorics,
Vol. 89,
Issue. ,
p.
103162.
Mudgal, Akshat
2020.
Arithmetic combinatorics on Vinogradov systems.
Transactions of the American Mathematical Society,
Vol. 373,
Issue. 8,
p.
5491.
Grechuk, Bogdan
2021.
Landscape of 21st Century Mathematics.
p.
51.
MUDGAL, AKSHAT
2021.
SUM-PRODUCT ESTIMATES FOR DIAGONAL MATRICES.
Bulletin of the Australian Mathematical Society,
Vol. 103,
Issue. 1,
p.
28.
Roche-Newton, O.
and
Warren, A.
2021.
Additive and multiplicative Sidon sets.
Acta Mathematica Hungarica,
Vol. 165,
Issue. 2,
p.
326.
Kerr, Bryce
2021.
Some multiplicative equations in finite fields.
Finite Fields and Their Applications,
Vol. 75,
Issue. ,
p.
101883.
Roche-Newton, Oliver
and
Warren, Audie
2021.
New Expander Bounds from Affine Group Energy.
Discrete & Computational Geometry,
Vol. 66,
Issue. 2,
p.
552.
RUDNEV, MISHA
and
STEVENS, SOPHIE
2022.
An update on the sum-product problem.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 173,
Issue. 2,
p.
411.
Dona, Daniele
2023.
A sum-bracket theorem for simple Lie algebras.
Journal of Algebra,
Vol. 631,
Issue. ,
p.
658.
Clevenger, Ginny Ray
Havard, Haley
Heard, Patch
Lott, Andrew
Rice, Alex
and
Wilson, Brittany
2025.
The sum-product problem for small sets.
Involve, a Journal of Mathematics,
Vol. 18,
Issue. 1,
p.
165.
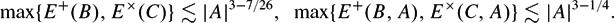 $
\begin{equation*}
\max\{E^+(B) , E^{\times}(C)\} \lesssim |A|^{3 - 7/26}, \ \ \max \{E^+(B,A) , E^{\times}(C, A) \}\lesssim |A|^{3 - 1/4}.
\end{equation*}
$
$
\begin{equation*}
\max\{E^+(B) , E^{\times}(C)\} \lesssim |A|^{3 - 7/26}, \ \ \max \{E^+(B,A) , E^{\times}(C, A) \}\lesssim |A|^{3 - 1/4}.
\end{equation*}
$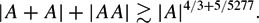 $
\begin{equation*}
|A+A| + |A A| \gtrsim |A|^{4/3 + 5/5277}.
\end{equation*}
$
$
\begin{equation*}
|A+A| + |A A| \gtrsim |A|^{4/3 + 5/5277}.
\end{equation*}
$