Hostname: page-component-669899f699-tpknm Total loading time: 0 Render date: 2025-04-26T00:38:41.827Z Has data issue: false hasContentIssue false
  • English
  • Français

On complete curves in moduli space I

Published online by Cambridge University Press:  24 October 2008

Gabino González Díez  and
William J. Harvey
Gabino González Díez
Affiliation:
Departamento de Matemáticas, Universidad Autónoma de Madrid, Spain
William J. Harvey
Affiliation:
Department of Mathematics, King's College London
Get access Rights & Permissions [Opens in a new window]

Extract

Let 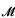g denote the moduli space of compact Riemann surfaces of genus g > 3. It is known that 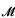g is a non-complete quasi-projective variety that contains many complete curves. This is because the Satake compactification 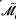g of 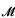g is projective and the boundary 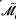\ 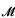has co-dimension 2; thus by intersecting 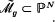with hypersurfaces in sufficiently general position one obtains a complete curve in 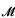g passing through any given set of points [8].

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 110 , Issue 3 , November 1991 , pp. 461 - 466
Copyright
Copyright © Cambridge Philosophical Society 1991

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

REFERENCES

[1]Atiyah, M. F.. The signature of fiber-bundles. In Global Analysis (University of Tokyo Press, 1969), pp. 73–84.Google Scholar
[2]Bers, L.. Uniformization, moduli, and Kleinian groups. J. London Math. Soc. 4 (1972), 257–300.CrossRefGoogle Scholar
[3]Diaz, S.. A bound on the dimension of complete subvarieties of g. Duke Math. J. 51 (1984), 405–408.CrossRefGoogle Scholar
[4]Griffiths, P. and Harris, J.. Principles of Algebraic Geometry (Wiley & Sons, 1978).Google Scholar
[5]Grauert, H. and Remmert, R.. Coherent Analytic Sheaves (Springer-Verlag, 1984).CrossRefGoogle Scholar
[6]Gilman, J.. On the moduli of compact Riemann surfaces with a finite number of punctures. In Discontinuous Groups and Riemann Surfaces, Ann. of Math. Studies no. 79 (Princeton University Press, 1974), pp. 181–205.CrossRefGoogle Scholar
[7]Gonzalez-Diez, G.. Loci of curves which are prime Galois coverings of P1. Proc. London Math. Soc. (3) 60 (1991), 469–489.CrossRefGoogle Scholar
[8]Harris, J.. Recent work on g. In Proceedings of International Congress of Mathematicians, Warsaw (PWN-Polish Scientific Publishers, 1983), pp. 719–726.Google Scholar
[9]Harvey, W. J.. Cyclic groups of automorphisms of a compact Riemann surface. Quart. J. Math. Oxford Ser. (2) 17 (1966), 86–97.CrossRefGoogle Scholar
[10]Harvey, W. J.. On branch loci in Teichmüller space. Trans. Amer. Math. Soc. 153 (1971), 387–399.Google Scholar
[11]Igusa, J.. Arithmetic variety of moduli for genus two. Ann. of Math. 72 (1960), 612–649.CrossRefGoogle Scholar
[12]Jones, G. A. and Singeeman, D.. Complex Functions (Cambridge University Press, 1987).CrossRefGoogle Scholar
[13]Kas, A.. On deformations of a certain type of irregular algebraic surfaces. Amer. J. Math. 90 (1968), 789–804.CrossRefGoogle Scholar
[14]Kodaira, K.. A certain type of irregular algebraic surface. J. Analyse Math. 19 (1967), 207–215.CrossRefGoogle Scholar
[15]Maclachlan, C.. and Harvey, W. J.. On mapping class groups and Teichmüller spaces. Proc. London Math. Soc. (3) 30 (1975), 496–512.CrossRefGoogle Scholar
[16]Miller, E. Y.. The homology of the mapping class group. J. Differential Geom. 24 (1986), 1–16.CrossRefGoogle Scholar
[17]Morita, S.. Characteristic classes of surface bundles I. Bull. Amer. Math. Soc. 11 (1984), 386–389.CrossRefGoogle Scholar
[18]Nag, S.. The Complex Analytic Theory of Teichmüller spaces (Wiley & Sons, 1988).Google Scholar
[19]Rauch, H. E.. A transcendental view of the space of algebraic Riemann surfaces. Bull. Amer. Math. Soc. 71 (1965), 1–39.CrossRefGoogle Scholar
[20]Riera, G.. Semi-direct products of Fuchsian groups and uniformization. Duke Math. J. 44 (1977), 291–304.CrossRefGoogle Scholar
[21]Shabat, G. B.. Local construction of complex algebraic surfaces with respect to the universal covering. Functional Anal. Appl. 17 (1983), 157–159.CrossRefGoogle Scholar