Hostname: page-component-78c5997874-v9fdk Total loading time: 0 Render date: 2024-11-19T03:56:19.602Z Has data issue: false hasContentIssue false
  • English
  • Français

On braid monodromies of non-simple braided surfaces

Published online by Cambridge University Press:  24 October 2008

Seiichi Kamada
Seiichi Kamada
Affiliation:
Department of Mathematics, Osaka City University, Osaka, 558, Japan
Get access Rights & Permissions [Opens in a new window]

Extract

A braided surface of degree m is a compact oriented surface S embedded in a bidisk 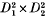such that 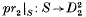is a branched covering map of degree m and 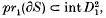, where 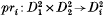is the projection. It was defined L. Rudolph [14, 16] with some applications to knot theory, cf. [13, 14, 15, 16, 17, 18]. A similar notion was defined O. Ya. Viro: A (closed) 2-dimensional braid in R4 is a closed oriented surface F embedded in R4 such that 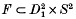and pr2 │F: F → S2 is a branched covering map, where 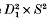is the tubular neighbourhood of a standard 2-sphere in R4. It is related to 2-knot theory, cf. [8, 9, 10]. Braided surfaces and 2-dimensional braids are called simple if their associated branched covering maps are simple. Simple braided surfaces and simple 2-dimensional braids are investigated in some articles, [5, 8, 9, 14, 16], etc. This paper treats of non-simple braided surfaces in the piecewise linear category. For braided surfaces a natural weak equivalence relation, called braid ambient isotopy, appears essentially although it is not important for classical dimensionai braids Artin's argument [1].

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 120 , Issue 2 , August 1996 , pp. 237 - 245
Copyright
Copyright © Cambridge Philosophical Society 1996

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Artin, E.. Theory of braids. Ann. of Math. 48 (1947), 101–126.CrossRefGoogle Scholar
[2]Berstein, I. and Edmonds, A. L.. On the construction of branched coverings of low-dimensional manifolds. Trans. Amer. Math. Soc. 247 (1979), 87–124.CrossRefGoogle Scholar
[3]Berstein, I. and Edmonds, A. L.. On the classification of generic branched coverings of surfaces. Illinois J. Math. Soc. 28 (1984), 64–82.Google Scholar
[4]Birman, J. S., Braids, links, and mapping class groups, Ann. Math. Studies 82 (Princeton Univ. Press, 1974).Google Scholar
[5]Carter, J. S. and Saito, M.. Knotted surfaces, braid movies and beyond; In Knots and Quantum Gravity, ed. Baez, J. (Clarendon Press, Oxford, to appear).Google Scholar
[6]Edmonds, A. L., Kulkarni, R. S. and Stong, R. E.. Realizability of branched coverings of surfaces. Trans. Amer. Math. Soc. 282 (1984), 773–790.CrossRefGoogle Scholar
[7]Fiedler, T.. A small state sum for knots. Topology 32 (1993), 281–294.CrossRefGoogle Scholar
[8]Kamada, S.. Surfaces in R 4 of braid index three are ribbon. J. Knot Theory Ramifications 1 (1992), 137–160.CrossRefGoogle Scholar
[9]Kamada, S.. A characterization of groups of closed orientable surfaces in 4-space. Topology 33 (1994), 113–122.CrossRefGoogle Scholar
[10]Kamada, S.. Alexander's and Markov's theorems in dimension four. Bull. Amer. Math. Soc. 31 (1994), 64–67.CrossRefGoogle Scholar
[11]Morton, H. R.. An irreducible 4-string braid with unknotted closure. Math. Proc. Cambridge Philos. Soc. 93 (1983), 259–261.CrossRefGoogle Scholar
[12]Murasugi, K.. On closed 3-braids (Amer. Math. Soc., 1974).CrossRefGoogle Scholar
[13]Rudolph, L.. Algebraic functions and closed braids. Topology 22 (1983), 191–202.CrossRefGoogle Scholar
[14]Rudolph, L.. Braided surfaces and Seifert ribbons for closed braids. Comment. Math. Helv. 58 (1983), 1–37.CrossRefGoogle Scholar
[15]Rudolph, L.. Some topologically locally-flat surfaces in the complex projectives plane. Comment. Math. Helv. 59 (1984), 592–599.CrossRefGoogle Scholar
[16]Rudolph, L.. Special positions for surfaces bounded closed braids. Rev. Mat. Iberoamericana 1 (1985), 93–133.CrossRefGoogle Scholar
[17]Rudolph, L.. A characterization of quasipositive Seifert surfaces (Constructions of quasipositive knots and links, III). Topology 31 (1992), 231–237.CrossRefGoogle Scholar
[18]Rudolph, L.. Quasipositivity as an obstruction to sliceness. Bull. Amer. Math. Soc. 29 (1993), 51–59.CrossRefGoogle Scholar