Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Ryshkov, S. S.
1974.
On the question of final ?-optimality of lattices providing the closest lattice packing of n-dimensional spheres.
Siberian Mathematical Journal,
Vol. 14,
Issue. 5,
p.
743.
1987.
Geometry of Numbers.
Vol. 37,
Issue. ,
p.
632.
Montgomery, Hugh L.
1988.
Minimal theta functions.
Glasgow Mathematical Journal,
Vol. 30,
Issue. 1,
p.
75.
Shushbaev, S. Sh.
1989.
Local minima of the Epstein zeta-function.
Mathematical Notes of the Academy of Sciences of the USSR,
Vol. 45,
Issue. 1,
p.
83.
Stein, Michael L.
1995.
Locally lattice sampling designs for isotropic random fields.
The Annals of Statistics,
Vol. 23,
Issue. 6,
Chiu, Patrick
1997.
Height of flat tori.
Proceedings of the American Mathematical Society,
Vol. 125,
Issue. 3,
p.
723.
Orlovskaya, E. V.
1997.
A minimum for the theta function in three variables and the solution of the Rankin-Sobolev problem in a three-dimensional space.
Journal of Mathematical Sciences,
Vol. 83,
Issue. 5,
p.
657.
Torquato, Salvatore
and
Stillinger, Frank H.
2003.
Local density fluctuations, hyperuniformity, and order metrics.
Physical Review E,
Vol. 68,
Issue. 4,
Sarnak, Peter
and
Strömbergsson, Andreas
2006.
Minima of Epstein’s Zeta function and heights of flat tori.
Inventiones mathematicae,
Vol. 165,
Issue. 1,
p.
115.
Lim, S. C.
and
Teo, L. P.
2008.
On the minima and convexity of Epstein zeta function.
Journal of Mathematical Physics,
Vol. 49,
Issue. 7,
Zachary, Chase E
and
Torquato, Salvatore
2009.
Hyperuniformity in point patterns and two-phase random heterogeneous media.
Journal of Statistical Mechanics: Theory and Experiment,
Vol. 2009,
Issue. 12,
p.
P12015.
Torquato, S.
2010.
Reformulation of the covering and quantizer problems as ground states of interacting particles.
Physical Review E,
Vol. 82,
Issue. 5,
Sandier, Etienne
and
Serfaty, Sylvia
2012.
From the Ginzburg-Landau Model to Vortex Lattice Problems.
Communications in Mathematical Physics,
Vol. 313,
Issue. 3,
p.
635.
Gruber, Peter M.
2012.
Application of an idea of Voronoĭ to lattice zeta functions.
Proceedings of the Steklov Institute of Mathematics,
Vol. 276,
Issue. 1,
p.
103.
Bétermin, Laurent
and
Zhang, Peng
2015.
Minimization of energy per particle among Bravais lattices in ℝ2: Lennard–Jones and Thomas–Fermi cases.
Communications in Contemporary Mathematics,
Vol. 17,
Issue. 06,
p.
1450049.
Rougerie, Nicolas
and
Serfaty, Sylvia
2016.
Higher‐Dimensional Coulomb Gases and Renormalized Energy Functionals.
Communications on Pure and Applied Mathematics,
Vol. 69,
Issue. 3,
p.
519.
Bétermin, Laurent
2016.
Two-Dimensional Theta Functions and Crystallization among Bravais Lattices.
SIAM Journal on Mathematical Analysis,
Vol. 48,
Issue. 5,
p.
3236.
Petrache, Mircea
and
Serfaty, Sylvia
2017.
NEXT ORDER ASYMPTOTICS AND RENORMALIZED ENERGY FOR RIESZ INTERACTIONS.
Journal of the Institute of Mathematics of Jussieu,
Vol. 16,
Issue. 3,
p.
501.
Bétermin, Laurent
and
Petrache, Mircea
2017.
Dimension reduction techniques for the minimization of theta functions on lattices.
Journal of Mathematical Physics,
Vol. 58,
Issue. 7,
Torquato, Salvatore
2018.
Hyperuniform states of matter.
Physics Reports,
Vol. 745,
Issue. ,
p.
1.


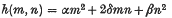
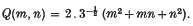
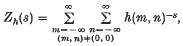
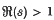 . The function
. The function 