No CrossRef data available.
On a class of non-measurable groups
Published online by Cambridge University Press: 24 October 2008
Extract
A group G will be called measurable if there exists a real-valued, non-negative set function μ(A) defined on all subsets A ⊂ G which satisfies 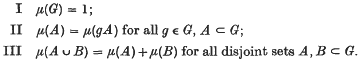 .
.
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 57 , Issue 2 , April 1961 , pp. 227 - 229
- Copyright
- Copyright © Cambridge Philosophical Society 1961
References
REFERENCES
(2)Mycielski, J., and Świerczkowski, S., On free groups of motions and decompositions of the Euclidean space. Fund. Math. 45 (1958), 283–91.CrossRefGoogle Scholar
(3)Von Neumann, J., Zur allgemeinen Theorie des Masses. Fund. Math. 13 (1929), 73–116.Google Scholar


