Hostname: page-component-586b7cd67f-dlnhk Total loading time: 0 Render date: 2024-11-26T14:52:32.040Z Has data issue: false hasContentIssue false
  • English
  • Français

A note on random walks in multidimensional time

Published online by Cambridge University Press:  24 October 2008

Janos Galambos  and
Imre Kátai
Janos Galambos
Affiliation:
Department of Mathematics, Temple University, Philadelphia, PA 19122, U.S.A.
Imre Kátai
Affiliation:
Institute of Mathematics, L. Eötvös University, Budapest 1088, Hungary
Get access Rights & Permissions [Opens in a new window]

Extract

Let Kr denote the set of r-tuples n = (n1, n2, …, nr), r ≥ 1, where the components ni are positive integers. Let {X, Xn, n ∈ Kr} be a family of independent and identically distributed random variables with positive mean EX = μ < + ∞ and finite variance VX = σ2 < + ∞. In a recent work, M. Maejima and T. Mori [2] have shown that, if X is integer valued, aperiodic and E∣X∣3 < + ∞, then, for r = 2 or 3,

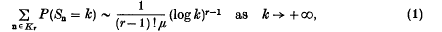
where

the summation being extended over all members j = (j1,j2, …, jr) of Kr that satisfy jt ≤ nt for all 1 ≤ t ≤ r.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 99 , Issue 1 , January 1986 , pp. 163 - 170
Copyright
Copyright © Cambridge Philosophical Society 1986

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Lavrik, A. F.. On the main terms of the divisor problem in the power series of the Riemann zeta function around its pole. (In Russian.) Trud. Mat. Inst. Akad. Nauk SSSR 142 (1976), 165–173.Google Scholar
[2]Maejima, M. and Mori, T.. Some renewal theorems for random walks in multidimensional time. Math. Proc. Cambridge Philos. Soc. 95 (1984), 149–154.CrossRefGoogle Scholar
[3]Petrov, V. V.. Sums of independent random variables (Springer, 1975).Google Scholar
[4]Ramachandra, K.. Some problems of analytic number theory. Acta Arithm. 31 (1976), 313–324.CrossRefGoogle Scholar
[5]Titchmarsh, E. C.. The theory of the Riemann zeta function (Oxford, 1951).Google Scholar