No CrossRef data available.
A note on a singular integral equation
Published online by Cambridge University Press: 24 October 2008
Extract
In his treatise entitled Introduction to the theory of Fourier integrals, E. C. Titchmarsh derives a Fourier transform of the solution of the integral equation
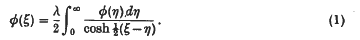
The transform of the solution given by him does not satisfy the Riemann-Lebesgue lemma, and further suffers from the defect that it has certain exponential properties which prevent the actual calculation of the function φ(ξ), since the inversion integral does not exist for all ξ > 0. We shall correct these defects and show further that the solution of (1) is particularly simple and that it can be expressed as the Legendre function of an order which depends on λ.
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 46 , Issue 2 , April 1950 , pp. 268 - 271
- Copyright
- Copyright © Cambridge Philosophical Society 1950
References
* Paley, and Wiener, , ‘Fourier transforms in the complex domain’, American Math. Soc. Publ. (1933, Chapter iv).Google Scholar
† Paley and Wiener, loc. cit. p. 51.
* It is clear that ø(ξ) vanishes for ξ < 0, since F_(w) is free of singularities in the lower half-plane 
and the path C may be closed in a fashion similar to the one we described for ξ > 0.
* A similar discussion of ψ(ξ) shows that ψ(ξ) = O(1) for ξ → 0− and O(e iξ) for ξ → − ∞, thus justifying the statement we made about F +(w).
* See, for example, Levine, and Schwinger, , ‘On the radiation of sound from an unflanged circular pipe’, Phys. Rev. 73 (1948), 383–406CrossRefGoogle Scholar, and Carlson, and Heins, , ‘The reflection of an electromagnetic plane wave by an infinite set of plates I and II’, Quart. Appl. Math. 4 (1947), 313–29CrossRefGoogle Scholar; 5 (1947), 82–8.