Norm form equations. III: positive characteristic
Published online by Cambridge University Press: 24 October 2008
Extract
This paper aims to provide a complete resolution of the general norm form equation over function fields of positive characteristic. In a previous paper [4] we studied norm forms in the simpler case of zero characteristic; that study forms the starting point for the present investigations. Diophantine problems over function fields of positive characteristic were first investigated by Armitage in 1968 [1], who clamied to have established an analogue of the Thue–Siegel–Roth–Uchiyama theorem for such fields. This claim was refuted by Osgood in 1975 [6], who also derived a correct analogue of Thue's approximation theorem. in 1983 a different attack was made on Diophantine problems over function fields, the principal weapon being a bound [2] for the heights of the solutions of the unit equation
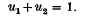
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 99 , Issue 3 , May 1986 , pp. 409 - 423
- Copyright
- Copyright © Cambridge Philosophical Society 1986
References
REFERENCES
- 6
- Cited by


