Hostname: page-component-586b7cd67f-t8hqh Total loading time: 0 Render date: 2024-11-26T07:43:43.290Z Has data issue: false hasContentIssue false
  • English
  • Français

Non-singular bilinear maps and stable homotopy classes of spheres

Published online by Cambridge University Press:  24 October 2008

Kee Yuen Lam
Kee Yuen Lam
Affiliation:
University of British Columbia, Vancouver
Get access Rights & Permissions [Opens in a new window]

Extract

A bilinear map ø Ra x Rb → Rc is non-singular if ø (x, y) = 0 implies x = 0 or y = 0. For background information on such maps see (4, 5, 6, 14). If we apply the ‘Hopf construction’ to ø, we get a map

defined by 2ø(x, y)) for all x ∈ Ra, y ∈ Rb satisfying ∥x∥2 + ∥y∥2 = 1. Homotopically, Jø coincides with the map obtained by first restricting and normalizing ø to , and then applying the standard Hopf construction ((13), p. 112). In any case, one gets an element [Jø] in , which in turn determines a stable homotopy class of spheres {Jø} in the d-stem 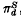, where d = a + b − c −1. An element in which equals {Jø} for some non-singular bilinear map ø will be called bilinearly representable. The first purpose of this paper is to prove

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 82 , Issue 3 , November 1977 , pp. 419 - 425
Copyright
Copyright © Cambridge Philosophical Society 1977

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Atiyah, M. F.Thom complexes. Proc. London Math. Soc. 11 (1961), 291–310.CrossRefGoogle Scholar
(2)Baum, P. F.Quadratic maps and the stable homotopy groups of spheres. Illinoia J. Math. (2) 4 (1967), 586–595.Google Scholar
(3)Kahn, D. S. and Priddy, S.Application of the transfer to stable homotopy theory. Bull. Amer. Math. Soc. 78 (1972), 981–987.CrossRefGoogle Scholar
(4)Lam, K. Y.On bilinear and skew-linear maps that are nonsingular. Quart. J. Math. Oxford (2) 19 (1968), 281–288.CrossRefGoogle Scholar
(5)Lam, K. Y.A note on Stiefel manifolds and the generalized J homomorphism. Bol. Soc. Mat. Mexicans. (In the Press.)Google Scholar
(6)Lam, K. Y.Some interesting examples of nonsingular bilinear maps. Topology 16 (1977), 185–188.CrossRefGoogle Scholar
(7)Milgram, R. J. and Zvengrowski, P.Skewness of r-fields on spheres. Topology 15 (1976), 325–335.CrossRefGoogle Scholar
(8)Milgram, R. J., Strutt, J. and Zvengrowski, P. Computing projective stable stems with the Adams spectral sequence. Preprint, to appear in. Quart. J. Math. Oxford.Google Scholar
(9)Mimura, M., Murai, J. and Nishida, G.Representing elements of stable homotopy groups by symmetric maps. Osaka J. Math. 11 (1974), 105–111.Google Scholar
(10)Mukai, J.An application of the Kahn-Priddy theorem. J. London Math. Soc. (In the Press.)Google Scholar
(11)Smith, L.Formes bilinéaires, homomorphisme J généralisé et groupes d'homotopie des sphères. C. R. Acad. Sci. Paris A 283 (1976), 825–827.Google Scholar
(12)Smith, L. Nonsingular bilinear forms, generalised J homomorphisms, and the homotopy of spheres, Parts I, II and III. (Preprint.)Google Scholar
(13)Toda, H.Composition methods in homotopy groups of spheres. Ann. of Math. Studies Princeton 49 (1962).Google Scholar
(14)Wood, R.Polynomial maps from spheres to spheres. Invent. Math. 5 (1968), 163–168.CrossRefGoogle Scholar