Hostname: page-component-586b7cd67f-gb8f7 Total loading time: 0 Render date: 2024-11-20T07:01:03.391Z Has data issue: false hasContentIssue false
  • English
  • Français

The New Action Function and the Unitary Field Theory

Published online by Cambridge University Press:  24 October 2008

L. Infeld
L. Infeld
Affiliation:
Lwów (John Casimirs University)
Get access Rights & Permissions [Opens in a new window]

Extract

A new form of the variation principle is given using the sum T of the Lagrangian L and the Hamiltonian 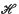as an action function. This new form of the variational principle enables us to find a new special action function, which conserves the chief features of Born's theory while changing some of its former results. To a given charge correspond two static solutions with central symmetry, one giving a finite, the other an infinite energy. The potential of the one (light) particle is analogous to that in Born's theory while the potential of the other resembles a potential barrier. Also, by using the new action function, the symmetry between electric and magnetic fields ceases to exist.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 32 , Issue 1 , January 1936 , pp. 127 - 137
Copyright
Copyright © Cambridge Philosophical Society 1936

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

† Born, , Proc. Roy. Soc. A, 143 (1934), 1410CrossRefGoogle Scholar; quoted here as I.

‡ Here and later we use the summation convention, i.e. where a suffix appears twice, we take the sum from 1 to 4.

§ Born, and Infeld, , Proc. Roy. Soc. A, 144 (1934), 144CrossRefGoogle Scholar; quoted as II.

∥ Schrödinger, , Proc. Roy. Soc. A, 150 (1935), 465.CrossRefGoogle Scholar

† are dual to fkl, Pkl. Although we consider here only the case of special relativity, we shall distinguish between covarian and contravariant tensors; the rule of raising and of lowering indices is: these operations on the index 4 do not change the value of the tensor component, that on one of the indices 1, 2, 3 changes only the sign.

‡ We put, here and later, for c (the velocity of light) and for b (the absolute field) the value 1, i. e. the time and the field components are to be measured in natural units.

† Our considerations correspond to the special case when L depends only on F and not on G.

† II, loc. cit. p. 436.

† We could also find (6·1) from putting (2·9) and (2·10) for L and .

‡ Schrödinger, loc. cit. Schrödinger formulated it for complex vectors, but it can easily be formulated for real tensors fkl, Pkl. It is the transformation

where a 2 + b 2 = 1.

† Mie, G., Ann. Physik, 40 (1913), 1.CrossRefGoogle Scholar

‡ II, loc. cit. p. 438.

† II, loc. cit. p. 446.