Hostname: page-component-586b7cd67f-g8jcs Total loading time: 0 Render date: 2024-11-26T20:40:24.651Z Has data issue: false hasContentIssue false
  • English
  • Français

Locally compact groups: maximal compact subgroups and N-groups

Published online by Cambridge University Press:  24 October 2008

R. W. Bagley ,
T. S. Wu  and
J. S. Yang
R. W. Bagley
Affiliation:
Department of Mathematics and Computer Science, University of Miami, Coral Gables, FL 33124, U.S.A.
T. S. Wu
Affiliation:
Department of Mathematics and Statistics, Case Western Reserve University, Cleveland, OH 44106, U.S.A.
J. S. Yang
Affiliation:
Department of Mathematics, University of South Carolina, Columbia, SC 29208, U.S.A.
Get access Rights & Permissions [Opens in a new window]

Abstract

If G is a locally compact group such that G/G0 contains a uniform compactly generated nilpotent subgroup, then G has a maximal compact normal subgroup K such that G/G is a Lie group. A topological group G is an N-group if, for each neighbourhood U of the identity and each compact set C ⊂G, there is a neighbourhood V of the identity such that 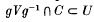for each g∈G. Several results on N-groups are obtained and it is shown that a related weaker condition is equivalent to local finiteness for certain totally disconnected groups.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 104 , Issue 1 , July 1988 , pp. 47 - 64
Copyright
Copyright © Cambridge Philosophical Society 1988

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Bagley, R. W. and Wu, T. S.. Maximal compact normal subgroups and pro-Lie groups. Proc. Amer. Math. Soc. 93 (1985), 373–376.CrossRefGoogle Scholar
[2]Bagley, R. W., Wu, T. S. and Yang, J. S.. On a class of topological groups more general than SIN groups. Pacific J. Math. 117 (1985), 209–217.CrossRefGoogle Scholar
[3]Bagley, R. W., Wu, T. S. and Yang, J. S.. Pro-Lie groups. Trans. Amer. Math. Soc. 287 (1985), 829–838.CrossRefGoogle Scholar
[4]Bagley, R. W. and Yang, J. S.. Locally invariant topological groups and semidirect products. Proc. Amer. Math. Soc. 93 (1985), 139–144.CrossRefGoogle Scholar
[5]Bagley, R. W. and Peyrovian, M. R.. A note on compact subgroups of topological groups. Bull. Austral. Math. Soc. 33 (1986), 273–278CrossRefGoogle Scholar
[6]Grosser, S., Loos, O. and Moskowitz, M.. Über Automorphismengruppen lokalkompakter Gruppen und Derivationen von Lie-Gruppen. Math. Z. 114 (1970), 321–339.CrossRefGoogle Scholar
[7]Grosser, S. and Moskowitz, M.. On central topological groups. Trans. Amer. Math. Soc. 127 (1967), 317–340.CrossRefGoogle Scholar
[8]Grosser, S. and Moskowitz, M.. Compactness conditions in topological groups. J. Reine Angew Math. 246 (1971), 1–40.Google Scholar
[9]Hall, M. Jr. The Theory of Groups (Macmillan, 1959).Google Scholar
[10]Hochschild, G.. The automorphism group of a Lie group. Trans. Amer. Math. Soc. 72 (1952), 209–216.Google Scholar
[11]Hofmann, K. H., Liukkonen, J. R. and Mislove, M. W.. Compact extensions of compactly generated nilpotent groups are pro-Lie. Proc. Amer. Math. Soc. 84 (1982), 443–448.CrossRefGoogle Scholar
[12]Iwasawa, K.. On some types of topological groups. Ann. of Math. (2) 50 (1949), 507–558.CrossRefGoogle Scholar
[13]Mostow, G. D.. Self-adjoint groups. Ann. of Math. (2) 62 (1955), 44–55.CrossRefGoogle Scholar
[14]Montgomery, D. and Zippin, L.. Topological Transformation Groups (Interscienee, 1955).Google Scholar
[15]Nachbin, L.. The Haar Integral (Van Nostrand, 1965).Google Scholar
[16]Peyrovian, M. R.. Maximal compact normal subgroups. Proc. Amer. Math. Soc. 99 (1987), 389–394.CrossRefGoogle Scholar
[17]Platonov, V. P.. Locally protectively nilpotent subgroups and nilelements in topological groups. Amer. Math. Soc. Transl. 66 (1968), 111–129.Google Scholar
[18]Platonov, V. P.. The structure of topological locally projectively nilpotent groups and groups with a normalizer condition. Mat. Sb. (N.S.) 114 (1967), 38–58.Google Scholar
[19]Raghunathan, M. S.. Discrete Subgroups of Lie Groups (Springer-Verlag, 1972).CrossRefGoogle Scholar
[20]Wang, S. P.. Compactness properties of topological groups. Trans. Amer. Math. Soc. 154 (1971), 301–314.CrossRefGoogle Scholar
[21]Wang, S. P.. Compactness properties of topological groups, II. Duke Math. J. 39 (1972), 243–251.CrossRefGoogle Scholar
[22]Wu, T. S.. A certain type of locally compact totally disconnected topological groups. Proc. Amer. Math. Soc. 23 (1969), 613–614.CrossRefGoogle Scholar
[23]Wu, T. S. and Yu, Y. K.. Compactness properties of topological groups. Michigan Math. J. 19 (1972), 299–313.CrossRefGoogle Scholar
[24]Yu, Y. K.. Topologically semisimple groups. Proc. London Math. Soc. (3) 33 (1976), 515–534.CrossRefGoogle Scholar