Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Beauzamy, Bernard
Enflo, Per
and
Wang, Paul
1994.
Quantitative Estimates for Polynomials in One or Several Variables.
Mathematics Magazine,
Vol. 67,
Issue. 4,
p.
243.
Beauzamy, Bernard
and
Dégot, Jérôme
1995.
Differential identities.
Transactions of the American Mathematical Society,
Vol. 347,
Issue. 7,
p.
2607.


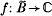 , analytic in
, analytic in 