Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Bojanowska, Agnieszka
1991.
Finite cyclic subgroups determine the spectrum of the equivariant 𝐾-theory.
Proceedings of the American Mathematical Society,
Vol. 113,
Issue. 1,
p.
245.
Lee, Chun-Nip
and
Minami, Norihiko
1994.
Algebraic Topology and Its Applications.
Vol. 27,
Issue. ,
p.
133.
Minami, Norihiko
1995.
The relative Burnside module and the stable maps between classifying spaces of compact Lie groups.
Transactions of the American Mathematical Society,
Vol. 347,
Issue. 2,
p.
461.


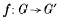
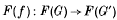 (
( ,
, 