Hostname: page-component-586b7cd67f-rcrh6 Total loading time: 0 Render date: 2024-11-23T07:35:05.150Z Has data issue: false hasContentIssue false
  • English
  • Français

A generalization of Abel summability

Published online by Cambridge University Press:  24 October 2008

B. Kuttner
B. Kuttner
Affiliation:
Christ's College
Get access Rights & Permissions [Opens in a new window]

Extract

The Abel sum of the series 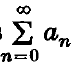can be written in the form

where

This suggests that we should define the “Abel limit”, as u → ∞, of any function A(u) as being given by the expression (1) whenever this exists. We shall, however, in this paper, restrict ourselves to functions A(u) which are bounded in any finite interval. Since we are concerned only with the behaviour of A(u) as u → ∞, this does not involve any serious loss of generality, while we avoid difficulties arising from the divergence of integrals at finite points. We note that the expression (1) can be written in the form

where

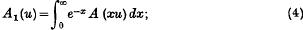
A1(u) may conveniently be described as the “Abel transform” of A(u).

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 32 , Issue 4 , December 1936 , pp. 541 - 559
Copyright
Copyright © Cambridge Philosophical Society 1936

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

* Landau, E., “Über die Konvergenz einiger Klassen von unendlichen Reihen am Rande des Konvergenzgebietes”, Monatshefte für Math. und Physik, 18 (1907), 8–28 (25–8)CrossRefGoogle Scholar.

* A (0) (u) is taken to mean A (u).

† The idea of combining Abel and Cesàro summability is not new. See, e.g. Lord, R. D., “On some relations between the Abel, Borel and Cesàro methods of summation”, Proc. London Math. Soc. (2), 38 (1935), 241–56.CrossRefGoogle Scholar In the definition there given, the Cesàro means are first formed, and then the Abel transform taken, instead of these processes being carried out in the reverse order, as here. But see § 2.2 of Lord's paper.

‡ Hardy, G. H., “Theorems relating to the summability and convergence of slowly oscillating series”, Proc. London Math. Soc. (2), 8 (1909), 310–20 (317).Google Scholar

* The contour of integration is not a straight line, but is such that | arg z | ≤ c < ½ on it in some neighbourhood of the origin. Otherwise the integral diverges at the origin.

* Schmidt, R., “Über divergente Folgen und lineare Mittelbildungen”, Math. Zeitschrift, 22 (1925), 89–152.CrossRefGoogle Scholar

† The case κ = 1 was given by Szász, O., “Verallgemeinerung eines Littlewoodschen Satzes, über Potenzreihen”, J. London Math. Soc. 3 (1928), 254–62.CrossRefGoogle Scholar For the general case, see, e.g., Lord, loc. cit., where a more general theorem is given.

‡ O., Szász, “Verallgemeinerung und neuer Beweis einiger Sätze Taubersche Art”, Münchener Sitzungsberichte, 1929, pp. 325–40.Google Scholar

* A simpler proof of this result is possible when κ ≥ 1, since we then have

* Wiener, N., “Tauberian theorems”, Annals of Maths. (2), 33 (1932), 1–100CrossRefGoogle Scholar (Theorem XV). In Wiener's result, we put

the result stated by Wiener is not quite equivalent to the result stated here, but only trivial modifications of the proof are needed.

* is the Cesàro mean of order κ of the series 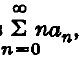whereas B (κ) (u) is evidently the Riesz mean.

† We require the result that, if then A 1 (u) is slowly decreasing, but the proof of this result presents no difficulty; in fact, the hypothesis implies that

* Steen, S. W. P., “Divisor functions”, Proc. London Math. Soc. (2), 31 (1930), 47–80CrossRefGoogle Scholar, and (2), 32 (1931), 356–68.

† is taken to mean K r (z).

* We use a dash to denote the differential coefficient of a function with respect to its argument.

* This method of summability is more often termed summability (A, λ), but such a nomenclature would obviously lead to confusion in the present paper.

* Cartwright, M. L., “On the relation between different types of Abel summation”, Proc. London Math. Soc. (2), 31 (1930), 81–96.CrossRefGoogle Scholar

† c is used to denote a constant; it may be a different constant at each occurrence.

* Wiener, loc. cit. (Theorem XXII).

† I am indebted to Prof. Hardy for suggesting this argument.

* It follows from (27) that the integral converges, except when t = 1.