Hostname: page-component-586b7cd67f-gb8f7 Total loading time: 0 Render date: 2024-11-29T21:19:56.193Z Has data issue: false hasContentIssue false
  • English
  • Français

The extremal values of Legendre polynomials and of certain related functions

Published online by Cambridge University Press:  24 October 2008

R. Cooper
R. Cooper
Affiliation:
The Queen's UniversityBelfast
Get access Rights & Permissions [Opens in a new window]

Extract

1. The tabulated values of the Legendre polynomials suggest that the right-hand minimum of Pn(x) changes monotonically as n increases. Let xr, n be the value of x which gives the rth extreme value to the left of 1 of Pn(x). Then we can show that

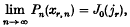
where jr is the rth pösitive zero of J1(z), and that after some term the sequence Pn(xr, n) is monotonic with the moduli of the terms decreasing. We cannot, however, show that the sequence is monotonic from the place at which its terms become significant.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 46 , Issue 4 , October 1950 , pp. 549 - 554
Copyright
Copyright © Cambridge Philosophical Society 1950

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

* The original title was ‘The extremal values of Legendre polynomials’. The paper was revised and extended because the referee suggested that if possible it should include a discussion of the associated Legendre function

† This was pointed out by John Todd, who has since studied the corresponding problem for Laguerre polynomials.

* In the following formulae a, b, c are certain constants depending on j, where explicit expressions are not needed; it can be verified that c = −j 2(j 2 − 12)/24.

† From the standard recurrence formulae, see for example, Whittaker, E. T. and Watson, G. N., Modern analysis (4th ed.) (Cambridge, 1927), p. 360, formula B.Google Scholar

* When ν = 1, the product is to be interpreted as unity.

† The notation is that used in Szegö, G., Orthogonal polynomials (New York, 1939)CrossRefGoogle Scholar; our formula (4·1) is quoted from p. 61 (4·21·2).

* We must include the term c/n 2 in the calculation, although the constant c disappears from the terms we calculate in our final result as it is multiplied by J α+1(j) = 0.

† See Hobson, E. W., Spherical and ellipsoidal harmonics (Cambridge, 1931), p. 219Google Scholar, formula 49, and the definition of for real values of x between − 1 and + 1 on p. 227.

* We require y to be positive.