Hostname: page-component-586b7cd67f-dlnhk Total loading time: 0 Render date: 2024-11-29T19:39:19.243Z Has data issue: false hasContentIssue false
  • English
  • Français

Entropy, Markov processes and Boltzmann's H-theorem

Published online by Cambridge University Press:  24 October 2008

P. A. P. Moran
P. A. P. Moran
Affiliation:
Australian National UniversityCanberra, A.C.T.
Get access Rights & Permissions [Opens in a new window]

Extract

Consider a Markov chain with a finite number of states E1,…,En and a transition matrix, (Pij), of probabilities of transition from state Ej to state Ei which is such that after some fixed finite number of steps, any state is accessible from any initial state. 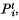Such a chain is said to be completely regular and it is easy to show that starting from any initial state, or distribution of states, the probabilities, , that the system is in state i after t steps, will converge to non-zero quantities, 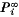, which are independent of the initial state. This condition of accessibility corresponds, in statistical mechanics, to the condition of ‘metrical transitivity’.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 57 , Issue 4 , October 1961 , pp. 833 - 842
Copyright
Copyright © Cambridge Philosophical Society 1961

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Ehrenfest, P. and Ehrenfest, T., Über zwei bekannte Einwände gegen das Boltzmannsche H-Theorem. Phys. Z. 8 (1907), 311–14.Google Scholar
(2)Kac, M., Probability and related topics in physical sciences (New York, 1959).Google Scholar
(3)Klein, M. J., Entropy and the Ehrenfest urn-model. Physica, 22 (1956), 569–75.CrossRefGoogle Scholar