Hostname: page-component-78c5997874-lj6df Total loading time: 0 Render date: 2024-11-19T17:54:15.897Z Has data issue: false hasContentIssue false
  • English
  • Français

Elliptic curves with good reduction away from 2: II

Published online by Cambridge University Press:  24 October 2008

R. G. E. Pinch
R. G. E. Pinch
Affiliation:
Emmanuel College, Cambridge
Get access Rights & Permissions [Opens in a new window]

Extract

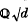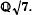In this paper we continue the study of elliptic curves defined over a quadratic field with good reduction at primes not dividing 2 begun in [9] (referred to as I). We extend the results of I to show that such a curve must have a point of order 2 also defined over when d = −7, −3, −2, −1, 2, 3 or 5 and list all such curves over .

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 100 , Issue 3 , November 1986 , pp. 435 - 457
Copyright
Copyright © Cambridge Philosophical Society 1986

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Abramowitz, M. and Stegun, I. A. (eds.). Handbook of Mathematical Functions (Dover, 1965).Google Scholar
[2]Birch, B. J. and Kuyk, W. (eds.). Modular Functions of One Variable IV. Lecture Notes in Mathematics, vol. 476 (Springer, 1975).CrossRefGoogle Scholar
[3]Birch, B. J. and Merriman, J.. Finiteness theorems for binary forms with given discriminant. Proc. London Math. Soc. (3) 24 (1972), 385–394.CrossRefGoogle Scholar
[4]Cremona, J. E.. Hyperbolic tesselations, modular symbols and elliptic curves over complex quadratic fields. Compositio Math. 51 (1984), 275–323.Google Scholar
[5]Hasse, H.. Number Theory. Grundlehren der math. Wissenschaften vol. 229 (Springer, 1980).CrossRefGoogle Scholar
[6]Merriman, J.. Binary forms and the reduction of curves. D.Phil, thesis (Oxford, 1970).Google Scholar
[7]Odlyzko, A.. Some analytic estimates of class numbers and discriminants. Invent. Math. 29 (1975), 275–286.CrossRefGoogle Scholar
[8]Ogg, A.. Elliptic curves and wild ramification. Amer. Math. J. 108 (1967), 1–21.CrossRefGoogle Scholar
[9]Pinch, R. G. E.. Elliptic curves with good reduction away from 2. Math. Proc. Cambridge Philos. Soc. 96 (1984), 25–38.CrossRefGoogle Scholar
[10]Pohst, M.. On the computation of number fields of small discriminant. J. Number Theory 14 (1982), 99–117.CrossRefGoogle Scholar
[11]Stewart, I. N. and Tall, D. O.. Algebraic Number Theory (Chapman & Hall, 1979).CrossRefGoogle Scholar
[12]Stroeker, R. J.. A class of Diophantine equations connected with certain elliptic curves over . Compositio Math. 38 (1979), 329–346.Google Scholar
[13]Stroeker, R. J.. Reduction of elliptic curves over imaginary quadratic number fields. Pacific J. Math. 108 (1983), 451–463.CrossRefGoogle Scholar
[14]Tate, J.. Algorithm for determining the type of a singular fibre in an elliptic pencil. In [2], 33–52.CrossRefGoogle Scholar
[15]Vaughan, T. P.. The discriminant of a quadratic extension of an algebraic field. Math. Comp. 40 (1983), 685–707.CrossRefGoogle Scholar
[16]Vaughan, T. P.. Corrigendum to [15]. Math. Comp. 43 (1984), 621.CrossRefGoogle Scholar
[17]Weiss, E.. Algebraic Number Theory (Chelsea, 1963).Google Scholar