Hostname: page-component-586b7cd67f-r5fsc Total loading time: 0 Render date: 2024-11-26T11:58:17.789Z Has data issue: false hasContentIssue false
  • English
  • Français

Eigenvalues of Composite Matrices

Published online by Cambridge University Press:  24 October 2008

Bernard Friedman
Bernard Friedman
Affiliation:
University of CaliforniaBerkeley
Get access Rights & Permissions [Opens in a new window]

Extract

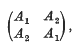Because of the symmetry of the problems encountered in the applications of matrices to physics, electrical engineering and numerical analysis, it frequently turns out that the matrix to be considered is a composite matrix, that is, a matrix whose elements are matrices. For example, the matrix may be where A1 and A2 are square matrices of order n which need not commute. It is easy to prove that the eigenvalues of this matrix of order 2n are the eigenvalues of the two matrices, A1+A2 and A1−A2 of order n.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 57 , Issue 1 , January 1961 , pp. 37 - 49
Copyright
Copyright © Cambridge Philosophical Society 1961

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Stéphanos, C., Sur une extension du calcul des substitutions lineaires. J. de Math. 4 (1900), 6.Google Scholar
(2)Williamson, J., The latent roots of a matrix of special type. Bull. Amer. Math. Soc. 37 (1931), 585.CrossRefGoogle Scholar
(3)Rutherford, D. E., Some continuant determinants arising in physics and chemistry. Proc. Roy. Soc. Edinb. sect. A, 62 (1947), 229.Google Scholar
(4)Egervary, E., On hypermatrices whose blocks are commutable in pairs and their applications in lattice dynamics. Acta Scient. Math. Szeged, 15 (1953), 211.Google Scholar
(5)Afriat, S. N., Composite matrices. Quart. J. Math. (2), 5 (1954), 81.CrossRefGoogle Scholar
(6)Friedman, B., Eigenvalues of compound matrices. N.Y.U. Math. Research Group Report, no. TW-16.Google Scholar
(7)MacDuffee, C. C., Theory of matrices. Ergebn Math. 2, no. 5 (1933).Google Scholar
(8)Albert, A. Adrian,. Modern higher algebra, Theorem 16, p. 238 (Chicago, 1937).Google Scholar
(9)Friedman, B., On n-commutative matrices. Math. Ann. 136 (1958), 343–7.CrossRefGoogle Scholar
(10)Kaufman, B., Crystal statistics. II. Phys. Rev. 76 (1949), 1232.CrossRefGoogle Scholar
(11)Muir, T., and Metzler, W., Theory of determinants, Chapter XII.Google Scholar