Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Shtern, A. I.
1987.
Duality for crossed products of von Neumann algebras.
Journal of Soviet Mathematics,
Vol. 37,
Issue. 6,
p.
1396.
1988.
Representations of *-Algebras, Locally Compact Groups, and Banach *-Algebraic Bundles: Basic Representation Theory of Groups and Algebras.
Vol. 125,
Issue. ,
p.
643.
1988.
Banach *-Algebraic Bundles, Induced Representations, and the Generalized Mackey Analysis.
Vol. 126,
Issue. ,
p.
1373.


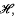 , and let
, and let 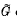 of
of 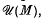 , the unitary group of
, the unitary group of 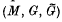 satisfies an additional axiom, we say that it is an extended covariant system. We define a Hilbert space
satisfies an additional axiom, we say that it is an extended covariant system. We define a Hilbert space  and operators
and operators 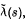 , acting on
, acting on 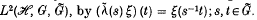 . The von Neumann algebra
. The von Neumann algebra 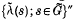 is then the covariance algebra of the extended covariant system
is then the covariance algebra of the extended covariant system 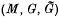 , denoted by
, denoted by 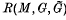 .
.