No CrossRef data available.
Article contents
Asymptotic identities for additive convolutions of sums of divisors
Published online by Cambridge University Press: 01 April 2022
Abstract
In a 1916 paper, Ramanujan studied the additive convolution
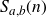 $S_{a, b}(n)$
of sum-of-divisors functions
$S_{a, b}(n)$
of sum-of-divisors functions
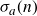 $\sigma_a(n)$
and
$\sigma_a(n)$
and
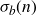 $\sigma_b(n)$
, and proved an asymptotic formula for it when a and b are positive odd integers. He also conjectured that his asymptotic formula should hold for all positive real a and b. Ramanujan’s conjecture was subsequently proved by Ingham, and then by Halberstam with a power saving error term.
$\sigma_b(n)$
, and proved an asymptotic formula for it when a and b are positive odd integers. He also conjectured that his asymptotic formula should hold for all positive real a and b. Ramanujan’s conjecture was subsequently proved by Ingham, and then by Halberstam with a power saving error term.
In this paper, we give a new proof of Ramanujan’s conjecture that obtains lower order terms in the asymptotics for most ranges of the parameters. We also describe a connection to a counting problem in geometric topology that was studied in the second author’s thesis and which served as our initial motivation in studying this sum.
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 174 , Issue 1 , January 2023 , pp. 59 - 78
- Copyright
- © The Author(s), 2022. Published by Cambridge University Press on behalf of Cambridge Philosophical Society


