No CrossRef data available.
Article contents
Asymptotic density in quasi-logarithmic additive number systems
Published online by Cambridge University Press: 01 March 2008
Abstract
We show that in quasi-logarithmic additive number systems 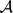 all partition sets have asymptotic density, and we obtain a corresponding monadic second-order limit law for adequate classes of relational structures. Our conditions on the local counting function p(n) of the set of irreducible elements of
all partition sets have asymptotic density, and we obtain a corresponding monadic second-order limit law for adequate classes of relational structures. Our conditions on the local counting function p(n) of the set of irreducible elements of  allow situations which are not covered by the density theorems of Compton [6] and Woods [15]. We also give conditions on p(n) which are sufficient to show the assumptions of Compton's result are satisfied, but which are not necessarily implied by those of Bell and Burris [2], Granovsky and Stark [8] or Stark [14].
allow situations which are not covered by the density theorems of Compton [6] and Woods [15]. We also give conditions on p(n) which are sufficient to show the assumptions of Compton's result are satisfied, but which are not necessarily implied by those of Bell and Burris [2], Granovsky and Stark [8] or Stark [14].
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 144 , Issue 2 , March 2008 , pp. 267 - 287
- Copyright
- Copyright © Cambridge Philosophical Society 2008


