No CrossRef data available.
An extension of the Ahlfors distortion theorem
Published online by Cambridge University Press: 24 October 2008
Extract
1. The conformal mapping of a strip domain in the z-plane on to a parallel strip— parallel, say, to the real axis of the ζ ( = ξ + iμ)-plane—brings about a certain distortion. More precisely: consider a cross-cut on the line ℜz = c joining the two sides of the frontier of the strip domain (in these introductory remarks we suppose for simplicity that there is only one such cross-cut on that line), and denote by ξ1(c) and ξ2(c) the lower and upper bounds of ξ on the image in the ζ-plane. The theorem of Ahlfors (1), now classical, states that
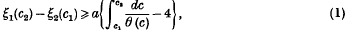
provided that

where a is the width of the parallel strip and θ(c) the length of the cross-cut.
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 50 , Issue 2 , April 1954 , pp. 261 - 265
- Copyright
- Copyright © Cambridge Philosophical Society 1954


