Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-24T01:43:49.994Z Has data issue: false hasContentIssue false
  • English
  • Français

Abstract Definitions for the Symmetry Groups of the Regular Polytopes, in Terms of Two Generators. Part I: The Complete Groups

Published online by Cambridge University Press:  24 October 2008

H. S. M. Coxeter  and
J. A. Todd
H. S. M. Coxeter
Affiliation:
Trinity College
J. A. Todd
Affiliation:
Trinity College
Get access Rights & Permissions [Opens in a new window]

Extract

The groups of rotations that transform the regular polygons and polyhedra into themselves have. been studied for many years. Lately, increasing interest has been shown in the “extended” groups, which include reflections (and other congruent transformations of negative determinant). Todd has proved that every such group can be defined abstractly in the form

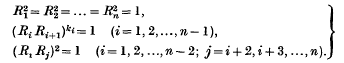
This group is denoted by [k1, k2, …, kn−1], and is the complete (extended) group of symmetries of either of the reciprocal n.-dimensional polytopes {k1, k2,…, kn−1}, {kn−1, kn−2,…, k1}. There is a sense in which these statements hold for arbitrarily large values of the k's. But here we are concerned only with the cases where the groups and the polytopes are finite. The finite groups are

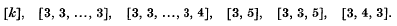
[k] is simply isomorphic with the dihedral group of order 2k (e.g. [2], the Vierergruppe). [3, 3,…, 3] with n − 1 threes, or briefly [3n−1], is simply isomorphic with the symmetric group of order (n + 1)!.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 32 , Issue 2 , May 1936 , pp. 194 - 200
Copyright
Copyright © Cambridge Philosophical Society 1936

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

* See, for instance, Motzok, , Mat. Sbornik, 40 (1933), 8–114.Google Scholar

† Todd, , “The groups of symmetries of the regular polytopes”, Proc. Camb. Phil. Soc. 27 (1931), 224.CrossRefGoogle Scholar Hereafter, we shall refer to this paper as G.S.R.P.

‡ Coxeter, , J. London Math. Soc. 10 (1935), 24;Google ScholarProc. Camb. Phil. Soc. 29 (1933), 1–7.Google Scholar

§ G.S.R.P. pp. 226–8.

║ Moore, E. H., Proc. London Math. Soc. (1), 28 (1897), 358.Google Scholar

* The symmetric group of degree five has two other elegant definitions:

As permutations, we may take

† This means that the symmetric group of degree n is

‡ Including [3, 6], the infinite group of the plane trigonal lattice.

§ Coxeter, , J. London Math. Soc. 9 (1934), 211.CrossRefGoogle Scholar

* Cf. Miller, G. A., Amer. J. Math. 33 (1911), 368, 369 (Degree 6, order 48; Degree 7, order 120). His s 1, s 2 are our p, Q.CrossRefGoogle Scholar

† When k = 3, this direct product is not [3, 3] but the pyritohedral group, for which Miller (loc. cit.) has given the simpler definition

‡ It follows that the abstract group (3) is infinite when k ≥ 6. When 2≤ k≤ 6, its order is the same as that of [3, k], namely 24k/(6–k).

§ G.S.R.P. p. 228.

* Cf. Moore, E. H., loc. cit.Google Scholar

† Or, writing R 2 in place of R,

* Burnside, W., Proc. London Math. Soc. (1), 28 (1897), 125.CrossRefGoogle Scholar

† Since the operations S 1 and S≡S 1S 2 … S n−1 generate the group [k 1, …, k n−1]′ except in the case of [3, 4, 3]′, the analysis given on p. 230 of G.S.R.P. for the unextended group is correct, except that for consistency of notation we ought to replace the symbols 1, …, n, 1′, …, n′ by n, …, 1, n′, …, 1′. But since the group [3n−2, 4]′ is generated in two distinct ways, according as we take it in the form [3n−2, 4]′ or [4, 3n−2]′, we can deduce a second representation, independent of the one previously given. We may in fact take

and then, if n is even,

If nis odd,