Hostname: page-component-586b7cd67f-l7hp2 Total loading time: 0 Render date: 2024-11-26T07:34:00.346Z Has data issue: false hasContentIssue false
  • English
  • Français

Absolute convexity in certain topological linear spaces

Published online by Cambridge University Press:  24 October 2008

I. J. Maddox  and
J. W. Roles
I. J. Maddox
Affiliation:
University of Lancaster
J. W. Roles
Affiliation:
University of Lancaster
Get access Rights & Permissions [Opens in a new window]

Extract

For r > 0 a non-empty subset U of a linear space is said to be absolutely r-convex if x, y ∈ U and |λ|r + |μ|r ≤ 1 together imply λx + μy∈ U, or, equivalently, xl, …, xn∈ U and

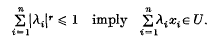
It is clear that if U is absolutely r-convex, then it is absolutely s-convex whenever s < r. A topological linear space is said to be r-convex if every neighbourhood of the origin θ contains an absolutely r-convex neighbourhood of the origin. For the case 0 < r ≤ 1, these concepts were introduced and discussed by Landsberg(2).

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 66 , Issue 3 , November 1969 , pp. 541 - 545
Copyright
Copyright © Cambridge Philosophical Society 1969

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Kelley, J. L., Namioka, I. et al. Linear topological spaces (Van Nostrand; Princeton, 1963).CrossRefGoogle Scholar
(2)Landsberg, M.Lineare topologische Räume, die nicht lokalconvex sind. Math. Z. 65 (1956), 104–12.CrossRefGoogle Scholar
(3)Maddox, I. J.Spaces of strongly summable sequences. Quart. J. Math. Oxford Ser. 18 (1967), 345–55.CrossRefGoogle Scholar
(4)Maddox, I. J.Paranormed sequence spaces generated by infinite matrices. Proc. Cambridge Philos. Soc. (1968).CrossRefGoogle Scholar
(5)Simons, S.The sequence spaces l(pv) and m(pv). Proc. London Math. Soc. (3), 15 (1965), 422–36.CrossRefGoogle Scholar