Hostname: page-component-586b7cd67f-rdxmf Total loading time: 0 Render date: 2024-11-26T14:23:02.491Z Has data issue: false hasContentIssue false
  • English
  • Français

The abelianization of a symmetric mapping class group

Published online by Cambridge University Press:  01 September 2009

MASATOSHI SATO
MASATOSHI SATO*
Affiliation:
Graduate School of Mathematical Sciences, The University of Tokyo, Komaba, Tokyo, 153-8914, Japan. e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Let Σg,r be a compact oriented surface of genus g with r boundary components. We determine the abelianization of the symmetric mapping class group 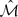(g,r)(p2) of a double unbranched cover p2: Σ2g − 1,2r → Σg,r using the Riemann constant, Schottky theta constant, and the theta multiplier. We also give lower bounds on the order of the abelianizations of the level d mapping class group.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 147 , Issue 2 , September 2009 , pp. 369 - 388
Copyright
Copyright © Cambridge Philosophical Society 2009

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Arbarello, E., Cornalba, M., Griffiths, P. A. and Harris, J.Geometry of Algebraic Curves. Vol. 1. (Springer-Verlag, 1985).CrossRefGoogle Scholar
[2]Birman, J. S. and Craggs, R.The μ-Invariant of 3-Manifolds and Certain Structural Properties of the Group of Homeomorphisms of a Closed, Oriented 2-Manifold. Trans. Amer. Math. Soc. 237 (1978), 283–309.Google Scholar
[3]Birman, J. S. and Hilden, H. M.On isotopies of homeomorphisms of Riemann surfaces. Ann. Math. 97 (3) (1973), 424–439.CrossRefGoogle Scholar
[4]Farb, B.Some problems on mapping class groups and moduli space, problems on mapping class groups and related topics. In Proc. Symp. Pure Math. 74 (2006), 11–55.CrossRefGoogle Scholar
[5]Farkas, H. M. and Rauch, H. E.Period relations of schottky type on Riemann surfaces. Ann. Math. 92 (3): (1970), 434–461.CrossRefGoogle Scholar
[6]Fay, J. D.Theta functions on Riemann surfaces. (Springer, 1973).CrossRefGoogle Scholar
[7]Hain, R. Torelli groups and geometry of moduli spaces of curves. Current Topics in Complex Algebraic Geometry (Clemens, CH and Kollar, J., eds.) MSRI Publications. 28 (1995), 97–143.Google Scholar
[8]Harer, J. L.The second homology group of the mapping class group of an orientable surface. Invent. Math. 72 (2) (1983), 221–239.CrossRefGoogle Scholar
[9]Harer, J. L.The rational Picard group of the moduli space of Riemann surfaces with spin structure. Contemp. Math. 150 (1993), 107–136.CrossRefGoogle Scholar
[10]Igusa, J.On the graded ring of theta-constants. Amer. J. Math. 86 (1) (1964), 219–246.CrossRefGoogle Scholar
[11]Igusa, J.Theta Functions (Springer, 1972).CrossRefGoogle Scholar
[12]Johnson, D.Homeomorphisms of a surface which act trivially on homology. Proc. Amer. Math. Soc. 75 (1) (1979), 119–125.CrossRefGoogle Scholar
[13]Johnson, D.An abelian quotient of the mapping class group g. Math. Ann. 249 (3) (1980), 225–242.CrossRefGoogle Scholar
[14]Johnson, D.Quadratic forms and the Birman–Craggs homomorphisms. Trans. Amer. Math. Soc. 261 (1) (1980), 235–254.CrossRefGoogle Scholar
[15]Johnson, D.The structure of the Torelli Group III: The abelianization of g. Topology, 24 (2) (1985), 127–144.CrossRefGoogle Scholar
[16]Lee, R., Miller, E. and Weintraub, S.The Rochlin invariant, theta functions and the holonomy of some determinant line bundle. J. Reine Angew. Math. 392 (1988), 187–218.Google Scholar
[17]McCarthy, J. D.On the first cohomology group of cofinite subgroups in surface mapping class groups. Topology 40 (2) (2000), 401–418.CrossRefGoogle Scholar
[18]Powell, J.Two theorems on the mapping class group of a surface. Proc. Amer. Math. Soc. 68 (3) (1978), 347–350.CrossRefGoogle Scholar