Hostname: page-component-78c5997874-mlc7c Total loading time: 0 Render date: 2024-11-16T17:20:02.409Z Has data issue: false hasContentIssue false
  • English
  • Français

Vieta-like products of nested radicals

Published online by Cambridge University Press:  23 January 2015

Thomas J. Osler
Thomas J. Osler*
Affiliation:
Mathematics Department, Rowan University, Glassboro, NJ 08028, USA, e-mail:[email protected]
Get access Rights & Permissions [Opens in a new window]

Extract

The beautiful infinite product of radicals

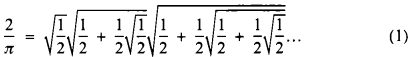
due to Vieta [1] in 1592, is one of the oldest non-iterative analytical expressions for π, In a previous paper [2] the author proved the following two Vieta-like products:

for N even, and

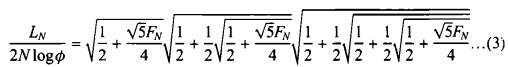
for N odd. Here N is a positive integer, FN and LN are the Fibonacci and Lucas numbers, and is the golden section. (The Fibonacci numbers are F1 = 1, F2 = 1, with the recursion relation 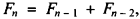, while the Lucas numbers are L1 = 1, L2 = 3 with the same recursion relation )

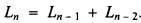Type
Articles
Information
The Mathematical Gazette , Volume 94 , Issue 529 , March 2010 , pp. 62 - 66
Copyright
Copyright © The Mathematical Association 2010

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Berggren, L., Borwein, J. and Borwein, P., Pi, a source book, Springer, New York (1997) pp. 53–67.Google Scholar
2. Osler, T. J., Vieta-like products of nested radicals with Fibonacci and Lucas numbers, Fibonacci Quarterly 45 (2008) pp. 202–204.Google Scholar
3. Vorob'ev, N. N., Fibonacci numbers, Pergamon Press (1961) pp. 20–28. AMS Classification Numbers: 40A20, IIB39.Google Scholar